The two shorter sides of right angles triangle are 5 cm and 12 cm. Let θ denote the angle opposite to the 5 cm side. Find sinθ,cosθ and tanθ.
To solve the problem, we need to find the values of sinθ, cosθ, and tanθ for a right triangle with shorter sides of lengths 5 cm and 12 cm, where θ is the angle opposite the side of length 5 cm.
Step 1: Identify the sides of the triangle
In a right triangle, we have:
- The side opposite to angle θ (which is 5 cm).
- The adjacent side (which is 12 cm).
- The hypotenuse (the longest side).
Step 2: Calculate the hypotenuse using the Pythagorean theorem
According to the Pythagorean theorem:
Hypotenuse2=Base2+Perpendicular2
Here, we can take:
- Base = 12 cm
- Perpendicular = 5 cm
Now, substituting the values:
Hypotenuse2=122+52=144+25=169
Taking the square root:
Hypotenuse=√169=13 cm
Step 3: Calculate sinθ
The sine of angle θ is given by the ratio of the length of the side opposite the angle to the length of the hypotenuse:
sinθ=OppositeHypotenuse=513
Step 4: Calculate cosθ
The cosine of angle θ is given by the ratio of the length of the adjacent side to the length of the hypotenuse:
cosθ=AdjacentHypotenuse=1213
Step 5: Calculate tanθ
The tangent of angle θ is given by the ratio of the length of the side opposite the angle to the length of the adjacent side:
tanθ=OppositeAdjacent=512
Final Answers
Thus, the values are:
- sinθ=513
- cosθ=1213
- tanθ=512
In a right triangle, we have:
- The side opposite to angle θ (which is 5 cm).
- The adjacent side (which is 12 cm).
- The hypotenuse (the longest side).
According to the Pythagorean theorem:
Hypotenuse2=Base2+Perpendicular2
Here, we can take:
- Base = 12 cm
- Perpendicular = 5 cm
Hypotenuse2=122+52=144+25=169
Taking the square root:
Hypotenuse=√169=13 cm
The sine of angle θ is given by the ratio of the length of the side opposite the angle to the length of the hypotenuse:
sinθ=OppositeHypotenuse=513
The cosine of angle θ is given by the ratio of the length of the adjacent side to the length of the hypotenuse:
cosθ=AdjacentHypotenuse=1213
The tangent of angle θ is given by the ratio of the length of the side opposite the angle to the length of the adjacent side:
tanθ=OppositeAdjacent=512
Thus, the values are:
- sinθ=513
- cosθ=1213
- tanθ=512
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example
61 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
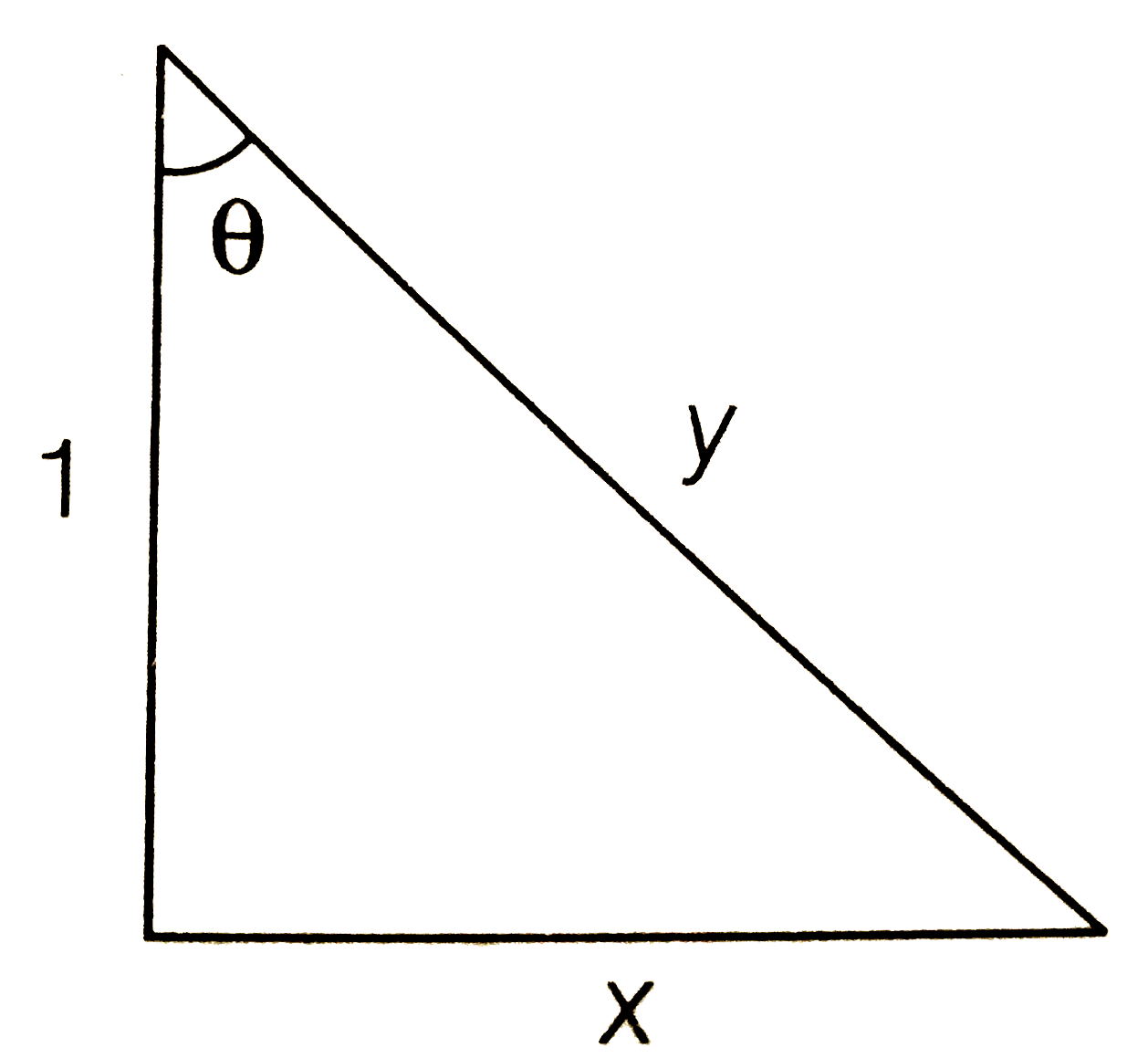
A right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionThe sides of a tringle are 8 cm, 10 cm and 12 cm. Prove that the greatest angle is double of the smalest angle.
View SolutionThe longest side of a right angled triangle is 4cm longer than one side and 2 cm longer than the other side. Find the longest side.
View SolutionIf two sides of a tringle are of length 5 cm and 1.5 cm, then the length of third side of the triangle cannot be
View SolutionThe area of the triangle whose sides. are 5 cm, 13 cm and 12 cm is
View SolutionTwo sides of a triangle are 12 cm and 14 cm. The perimeter of the triangle is 36 cm. What is its third side?
View SolutionTwo sides of a triangles are 12 cm and 7 cm , find the range for the length of its third side.
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is right-angled triangle.
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is a right-angle triangle.
View SolutionThe sides containing right angle of a right angled triangle are 8 cm and 6 cm. It is rotated about the side of 8 cm. Find the total surface area of the formed solid.
View Solution
