Four particles of masses m,2m,3m,4m are placed at corners of a square of side 'a' as shown in fig. Find out coordinateds of centre of mass.
The correct Answer is:(a2,7a10)
To find the coordinates of the center of mass of the four particles placed at the corners of a square, we can follow these steps:
Step 1: Define the positions of the particles
Let's place the square in the coordinate system. We can assign the following coordinates to the corners of the square:
- Particle 1 (mass = m) at (0, 0)
- Particle 2 (mass = 2m) at (a, 0)
- Particle 3 (mass = 3m) at (a, a)
- Particle 4 (mass = 4m) at (0, a)
Step 2: Calculate the total mass
The total mass M of the system is the sum of the individual masses:
M=m+2m+3m+4m=10m
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass xcm is given by the formula:
xcm=∑mixi∑mi
Substituting the values:
xcm=m⋅0+2m⋅a+3m⋅a+4m⋅010m
This simplifies to:
xcm=(0+2ma+3ma+0)10m=5ma10m=a2
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass ycm is given by:
ycm=∑miyi∑mi
Substituting the values:
ycm=m⋅0+2m⋅0+3m⋅a+4m⋅a10m
This simplifies to:
ycm=(0+0+3ma+4ma)10m=7ma10m=7a10
Step 5: Final coordinates of the center of mass
Thus, the coordinates of the center of mass are:
(a2,7a10)
Summary
The coordinates of the center of mass of the four particles are:
(a2,7a10)
Let's place the square in the coordinate system. We can assign the following coordinates to the corners of the square:
- Particle 1 (mass = m) at (0, 0)
- Particle 2 (mass = 2m) at (a, 0)
- Particle 3 (mass = 3m) at (a, a)
- Particle 4 (mass = 4m) at (0, a)
The total mass M of the system is the sum of the individual masses:
M=m+2m+3m+4m=10m
The x-coordinate of the center of mass xcm is given by the formula:
xcm=∑mixi∑mi
Substituting the values:
xcm=m⋅0+2m⋅a+3m⋅a+4m⋅010m
This simplifies to:
xcm=(0+2ma+3ma+0)10m=5ma10m=a2
The y-coordinate of the center of mass ycm is given by:
ycm=∑miyi∑mi
Substituting the values:
ycm=m⋅0+2m⋅0+3m⋅a+4m⋅a10m
This simplifies to:
ycm=(0+0+3ma+4ma)10m=7ma10m=7a10
Thus, the coordinates of the center of mass are:
(a2,7a10)
The coordinates of the center of mass of the four particles are:
(a2,7a10)
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-IV B
Explore 14 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V A
Explore 20 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
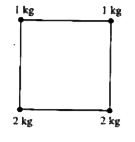
Four point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View SolutionFour particles, each of mass 1kg, are placed at the corners of a square OABC of side 1m. 'O' is at the origin of the coordinate system. OA and OC are aligned along positive x-axis and positive y-axis respectively. The position vector of the centre of mass is (in 'm')
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
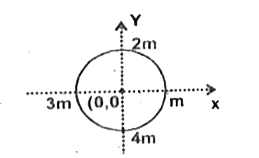
View SolutionFour particles of masses m, 2m, 3m & 4m respectively are placed on the periphery of a circle of radius R as shown in the figure then CM of the system contains the particle is at
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles. Assume that D is situated at the origin.
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is

View Solution
