After climbing a wall of 3m height, a person of weight W jumps to the ground. If the body comes to a complete stop in 0.15s. After the feet touch the ground, calculate the average impulsive force in the vertical direction exerted by ground on the feet.
5W
5.21W
3W
6W
The correct Answer is:B
To solve the problem step by step, we need to calculate the average impulsive force exerted by the ground on the feet of a person who jumps from a height of 3 meters and comes to a stop in 0.15 seconds.
Step 1: Calculate the speed just before hitting the ground
To find the speed of the person just before touching the ground, we can use the principle of energy conservation or kinematic equations. The potential energy at the height will convert into kinetic energy just before impact.
Using the equation:
v=√2gh
where:
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height (3 m).
Substituting the values:
v=√2⋅9.81⋅3=√58.86≈7.67m/s
Step 2: Calculate the change in momentum
The change in momentum (ΔP) can be calculated using the formula:
ΔP=Pfinal−Pinitial=0−mv
Since the person comes to a complete stop, the final momentum is 0. The initial momentum is mv, where m is the mass of the person. Thus:
ΔP=0−mv=−mv⟹ΔP=mv
Step 3: Calculate the average impulsive force
The average impulsive force (Faverage) can be calculated using the formula:
Faverage=ΔPΔt
where Δt is the time taken to stop (0.15 s). Substituting the values:
Faverage=mv0.15
Step 4: Substitute m with weight W
Since weight W is given by W=mg, we can express mass m as m=Wg. Substituting this into the force equation gives:
Faverage=(W/g)v0.15
Step 5: Substitute v
Now substitute v from Step 1:
Faverage=(W/g)⋅7.670.15
Step 6: Calculate the average impulsive force
Substituting g≈9.81m/s2:
Faverage=(W/9.81)⋅7.670.15
Calculating this gives:
Faverage≈5.21W
Thus, the average impulsive force exerted by the ground on the feet is approximately 5.21W.
Final Answer
The average impulsive force in the vertical direction exerted by the ground on the feet is 5.21W.
---
To find the speed of the person just before touching the ground, we can use the principle of energy conservation or kinematic equations. The potential energy at the height will convert into kinetic energy just before impact.
v=√2gh
where:
- g is the acceleration due to gravity (approximately 9.81m/s2),
- h is the height (3 m).
v=√2⋅9.81⋅3=√58.86≈7.67m/s
The change in momentum (ΔP) can be calculated using the formula:
ΔP=Pfinal−Pinitial=0−mv
Since the person comes to a complete stop, the final momentum is 0. The initial momentum is mv, where m is the mass of the person. Thus:
ΔP=0−mv=−mv⟹ΔP=mv
The average impulsive force (Faverage) can be calculated using the formula:
Faverage=ΔPΔt
where Δt is the time taken to stop (0.15 s). Substituting the values:
Faverage=mv0.15
Since weight W is given by W=mg, we can express mass m as m=Wg. Substituting this into the force equation gives:
Faverage=(W/g)v0.15
Now substitute v from Step 1:
Faverage=(W/g)⋅7.670.15
Substituting g≈9.81m/s2:
Faverage=(W/9.81)⋅7.670.15
Calculating this gives:
Faverage≈5.21W
The average impulsive force in the vertical direction exerted by the ground on the feet is 5.21W.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A body is thrown vertically upwards from the ground. It reaches a maximum height of 20m in 5s. After what time it will reach the ground from its maximum height position ?
View SolutionA man whose mass is m kg jumps vertically into air from the sitting position in which his centre of mass is at a height h1 from the ground. When his feet are just about to leave the ground his centre of mass is at height h2 from the ground and finally centre of mass rises to h3 above the ground when he is at the top of the jump. what is the average upward force exerted by the ground on him?
View Solution
Knowledge Check
- Question 1 - Select One
As shown in the figure below, Tony has determined that he must ride his skateboard down a long ramp to be able to jump a shorter ramp with enough time to complete a new trick. First, he needs to determine the dimensions of both the shorter and longer ramps. Tony is on his skateboard at point K, 20 feet above the ground . He then notes that the vertical height ¯¯¯¯¯¯HJ of the shorter ramp is 6 feet above the ground, and the length of the shorter ramp ¯¯¯¯¯¯GJ is 9 feet. Approximately how many feet long is the longer ramp ?
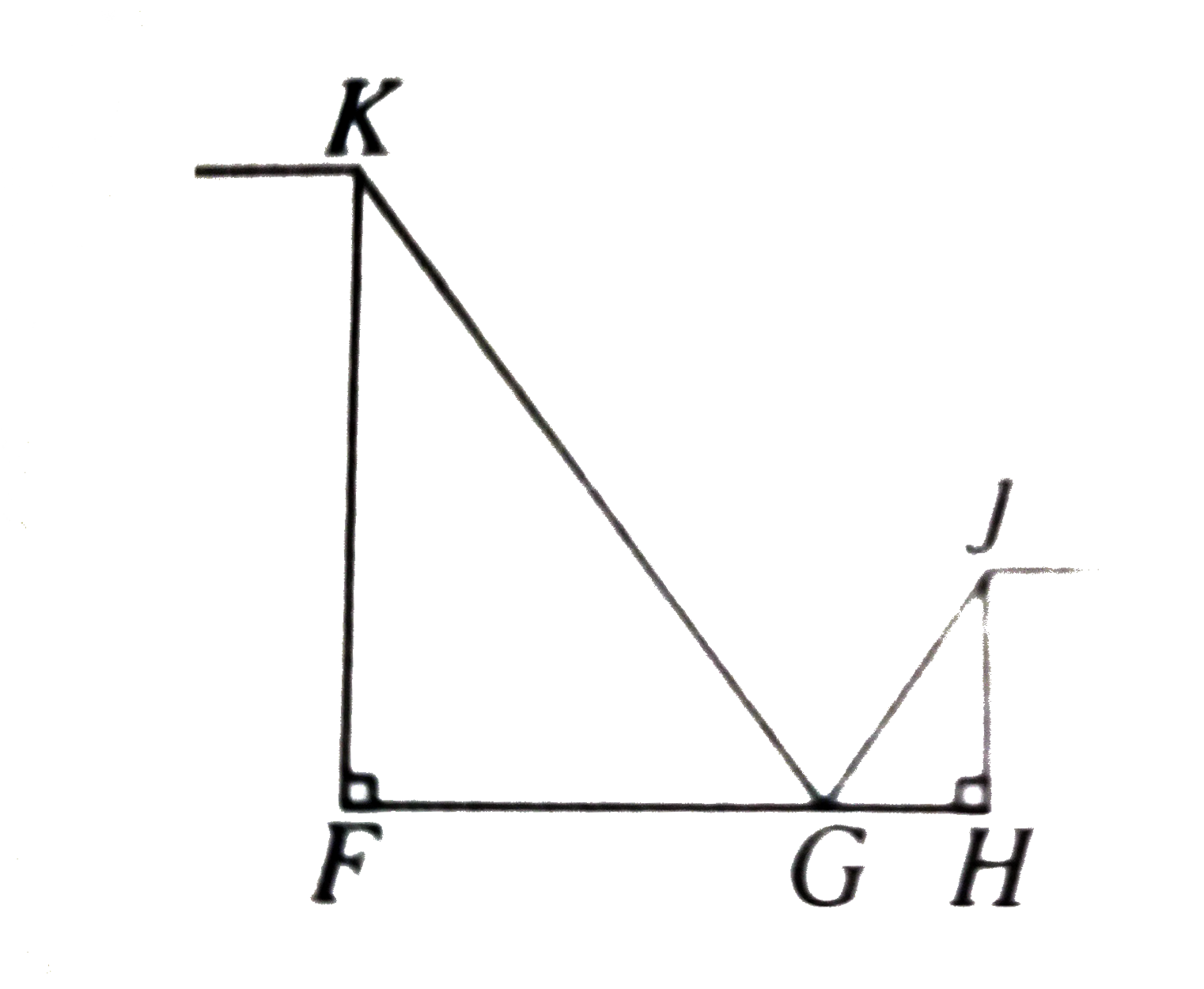 A3B12C15D30
A3B12C15D30
A ball of mass 1 kg is dropped from height 9.8 m, strikes with ground and rebounds at height 4.9 m, if the time of contact between ball and ground is 0.1 s then find impulse and average force acting on ball.
View SolutionA rubber ball of mass 50 g falls from a height of 5m and rebounds to a height of 1.25 m. Find the impulse and the average force between the ball and the ground if the time for which they are in contact was 0.1s
 View Solution
View SolutionA rubber ball of mass 0.4 kg hits the ground at same angle without any change in speed . If the speed of ball is 1 m/s and the period of contact between the ball and floor is 0.4 s, find the average force exerted by the ball on the ground .
View SolutionAn 80 kg stuntman jumps out of a window that's 45m above the ground
Q. He lands on a large, air-filled target, coming to rest in 1.5 s. what average force does he feel while coming to rest?View SolutionA man of mass m climbs to a rope ladder suspended below a balloon of mass M. The balloon is stationary with respect to the ground.
(a) If the man begins to climb the ladder at speed v (with respect to the ladder), in what direction and with what speed (with respect to the ground) will the balloon move?
(b) What is the state of the motion after the man stops climbing?View SolutionA body is thrown vertically up reaches a maximum height of 78.4 m. After what time it will reach the ground from the maximum height reached ?
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 ms−1 . The ball reaches the ground after 5s. Calculate the height of the tower .
View Solution
