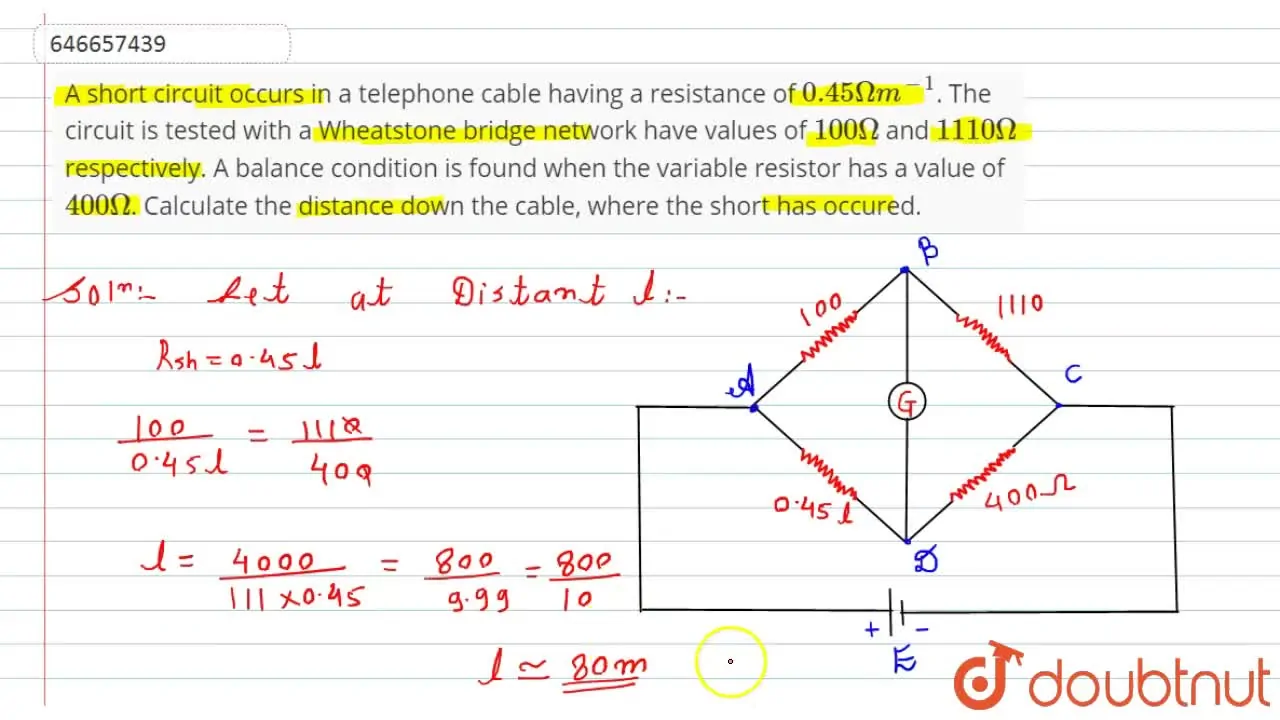
A short circuit occurs in a telephone cable having a resistance of 0.45Ωm−1. The circuit is tested with a Wheatstone bridge network have values of 100Ω and 1110Ω respectively. A balance condition is found when the variable resistor has a value of 400Ω. Calculate the distance down the cable, where the short has occured.
The correct Answer is:40 m
1000.45l=1110400⇒l=40m
_E01_263_S01.png)
Related Playlists
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(A)16videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-289videos
KINEMATICS
Similar Questions
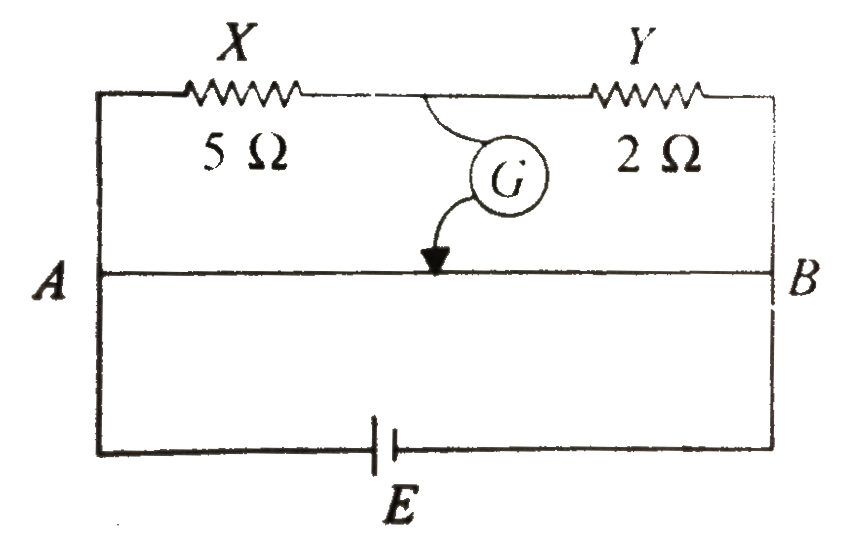
In the simple potentionmeter circuit, where the length AB of the potentiometer wire is 1m, the resistors X and Y have values of 5Ω and 2Ω, respectively. When X is shunted by a wire, the balance point is found to be 0.625m from A. What is the resistance of the shunt?
 View Solution
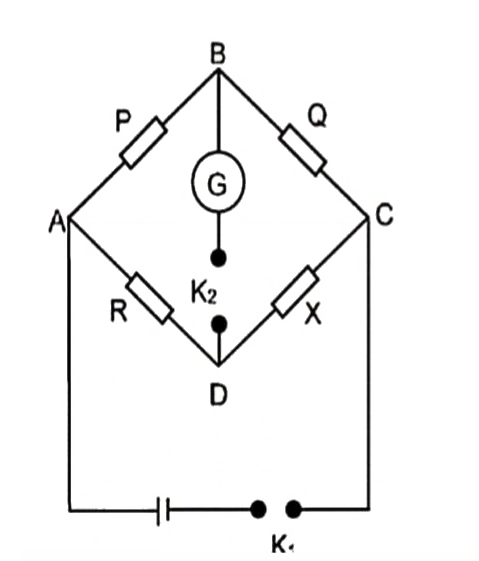
View SolutionThe figure below shows a wheatstone bridge with resistors P and Q having almost equal resistance. When R = 400Ω , the bridge is in balanced condition. If on interchanging P and Q, the bridge is again balanced for R=405Ω, then the value of X is
 View Solution
View SolutionDraw the circuit for experimental verification of Ohm's law using a source of variable DC voltage, a main resistance of 100Ω, two galvanometers and two resistances of value 106Ω and 10−3Ω respectively. Clearly show the positions of the voltmeter and the ammeter.
View SolutionDraw the circuit for experimental verfication of Ohm's law using a source of variable DC voltage, a main resistance of 100(Ω), two galvanometers and two resistances of values 106Ω and 10−3 respectively. Clearly show the positions of the voltmeter and the ammeter.
View SolutionA battery of emf E0=12V is connected across a 4m long uniform wire having resistance 4Ωm. The cells of small
emfs ε1=2V and ε2−4V having internal resistance 2Ω and 6Ω respectively, are connected as shown in the figure. If galvanometer shows no deflection at the point N, the distance of point N from teh point A is equal to
 View Solution
View SolutionFour resistances of 3Ω,3Ω,3Ωand4Ω respectively are used to form a Wheatstone bridge. The 4Ω resistance is short circuited with a resistance R in order to get bridge balanced. The value of R will be
View SolutionFour resistors A, and D form a Wheatstone bridge.
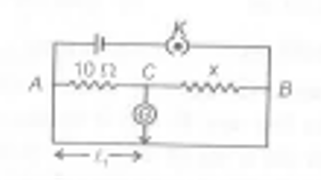
The bridge is balanced , when C = 100Ω If A and B are interchanged the bridge balances for C=121Ω. The value of D isView SolutionThe resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
 View Solution
View SolutionA cell can be balanced against 110cm and 100cm of potentiometer wire, respectively with and without being short circuited through a resistance of 10Ω. Its internal resistance is
View SolutionA cell can be balanced against 110cm and 100cm of potentiometer wire, respectively with and without being short circuited through a resistance of 10Ω. Its internal resistance is
View Solution