A transverse wave travelling along the positive x-axis, given by y=Asin(kx−ωt) is superposed with another wave travelling along the negative x-axis given by y=Asin(kx+ωt). The point x=0 is
a node
an antinode
neither a node nor an antinode
a node or antinode depending on t
The correct Answer is:B
To solve the problem, we need to analyze the superposition of two waves traveling in opposite directions along the x-axis.
1. Identify the Waves:
We have two waves:
- Wave 1 traveling in the positive x-direction:
y1=Asin(kx−ωt)
- Wave 2 traveling in the negative x-direction:
y2=Asin(kx+ωt)
2. Evaluate at x=0:
We need to find the resultant wave at the point x=0.
- For Wave 1:
y1(0,t)=Asin(0−ωt)=Asin(−ωt)=−Asin(ωt)
- For Wave 2:
y2(0,t)=Asin(0+ωt)=Asin(ωt)
3. Superpose the Waves:
Now, we add the two waves together at x=0:
y(0,t)=y1(0,t)+y2(0,t)=−Asin(ωt)+Asin(ωt)
This simplifies to:
y(0,t)=0
4. Interpret the Result:
The resultant wave at x=0 is zero, which indicates that there is complete destructive interference at this point.
5. Determine the Nature of the Point:
Since the amplitude is zero at x=0, this point is a node (where the amplitude is minimum).
Conclusion:
Thus, the point x=0 is a node.
We have two waves:
- Wave 1 traveling in the positive x-direction:
y1=Asin(kx−ωt)
- Wave 2 traveling in the negative x-direction:
y2=Asin(kx+ωt)
We need to find the resultant wave at the point x=0.
- For Wave 1:
y1(0,t)=Asin(0−ωt)=Asin(−ωt)=−Asin(ωt)
- For Wave 2:
y2(0,t)=Asin(0+ωt)=Asin(ωt)
Now, we add the two waves together at x=0:
y(0,t)=y1(0,t)+y2(0,t)=−Asin(ωt)+Asin(ωt)
This simplifies to:
y(0,t)=0
The resultant wave at x=0 is zero, which indicates that there is complete destructive interference at this point.
Since the amplitude is zero at x=0, this point is a node (where the amplitude is minimum).
Thus, the point x=0 is a node.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A travelling wave represented by
y=Asin(ωt−kx)
is superimposed on another wave represented by
y=Asin(ωt+kx). The resultant isAstanding wave having nodes at x=(n+12)λ2, n=0,1,2,….Bsatnding wave having nodes at x=nλ2,n=0,1,2..Cwave travelling along +x directionDwave travelling along-x direction
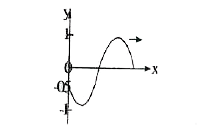
The equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by
View SolutionIn a wave motion y=asin(kx−ωt),y can represent :-
View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by

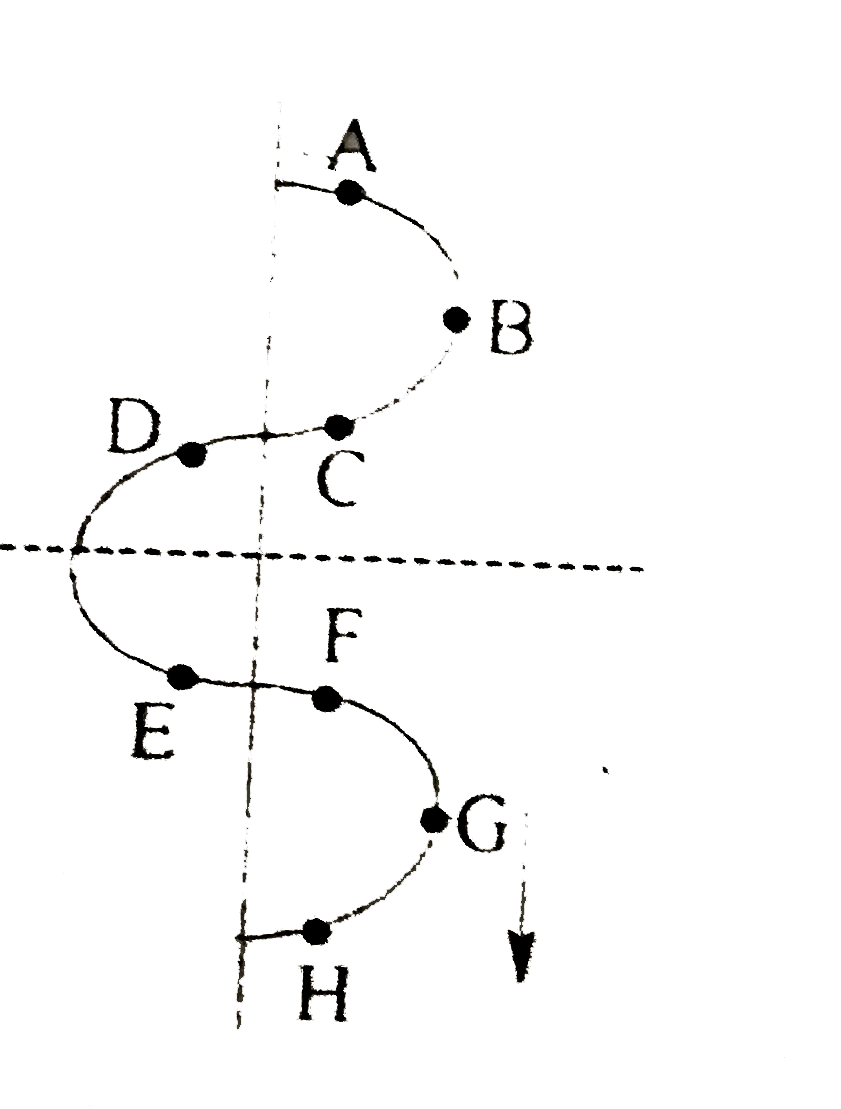
View SolutionA transverse wave travelling along negativ y-axis its snap shot is given at any instant of tie t. points which is having velocity in negative x-direction.
View SolutionA progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:
View SolutionA progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:

View SolutionThe position of a transverse wave travelling in medium along positive x-axis is shown in figure at time t=0. Speed of wave is v=200 m/s
Frequency of the wave is

View Solution