Two tuning forks A and B lying on opposite sides of observer 'O' and of natural frequency 80Hz move with velocity 10m/s relative to stationary observer O. Fork A moves away from the observer while the fork B moves towards him. A wind with a speed 10m/s is blowing in the direction of motion of fork A. Find the beat frequency measured by the observer in Hz. [Take speed of sound in air as 340m/s].
5
6
7
8
The correct Answer is:A
To find the beat frequency measured by the observer due to the two tuning forks A and B, we will follow these steps:
Step 1: Understand the Problem
We have two tuning forks, A and B, both with a natural frequency of 80 Hz. Fork A is moving away from the observer O, while fork B is moving towards the observer. There is also wind blowing from B to A at a speed of 10 m/s. We need to calculate the frequencies heard by the observer from both tuning forks and then find the beat frequency.
Step 2: Calculate the Effective Speed of Sound
The speed of sound in air is given as 340 m/s. However, since there is wind blowing in the direction of fork A, we need to adjust the effective speed of sound for fork A.
- For fork A moving away from the observer:
vA=vsound−vwind=340m/s−10m/s=330m/s
Step 3: Calculate the Frequency Heard from Fork A
Using the Doppler effect formula for a source moving away from the observer:
fA=(vsound−vwindvsound−vsource)f0
Substituting the values:
- vsound=340m/s
- vwind=10m/s
- vsource=10m/s
- f0=80Hz
fA=(330340−10)×80=(330330)×80=80Hz
Step 4: Calculate the Frequency Heard from Fork B
For fork B moving towards the observer:
fB=(vsound+vwindvsound+vsource)f0
Substituting the values:
- vsound=340m/s
- vwind=10m/s
- vsource=10m/s
fB=(340+10340+10)×80=(350350)×80=80Hz
Step 5: Calculate the Beat Frequency
The beat frequency is given by the absolute difference between the two frequencies:
fbeat=|fA−fB|
Substituting the values:
fbeat=|80−80|=0Hz
Conclusion
The beat frequency measured by the observer is 0 Hz.
---
We have two tuning forks, A and B, both with a natural frequency of 80 Hz. Fork A is moving away from the observer O, while fork B is moving towards the observer. There is also wind blowing from B to A at a speed of 10 m/s. We need to calculate the frequencies heard by the observer from both tuning forks and then find the beat frequency.
The speed of sound in air is given as 340 m/s. However, since there is wind blowing in the direction of fork A, we need to adjust the effective speed of sound for fork A.
vA=vsound−vwind=340m/s−10m/s=330m/s
Using the Doppler effect formula for a source moving away from the observer:
fA=(vsound−vwindvsound−vsource)f0
Substituting the values:
- vsound=340m/s
- vwind=10m/s
- vsource=10m/s
- f0=80Hz
For fork B moving towards the observer:
fB=(vsound+vwindvsound+vsource)f0
Substituting the values:
- vsound=340m/s
- vwind=10m/s
- vsource=10m/s
The beat frequency is given by the absolute difference between the two frequencies:
fbeat=|fA−fB|
Substituting the values:
fbeat=|80−80|=0Hz
The beat frequency measured by the observer is 0 Hz.
Topper's Solved these Questions
Similar Questions
Two tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
View SolutionTwo tuning forks with natural frequencies 340HZ each move relative to a stationary observer . One forks moves away from the oberver while the other moves towards him at the same speed . The observer hears beats of frequency 3HZ . Find the speed the of the tuning fork (velocity of sound in air is 340m/s) .
View Solutiona bus is moving towards and stationary observer with speed 20 m/s blows a horn of frequency 200 Hz. the frequency of sound heard by the observer is approximately ( take speed of sound 320 m/s)
View SolutionA source of sound is travelling with a velocity of 30ms towards a stationary observer. If actual frequency of source is 1000 Hz and the wind is blowing with velocity 20ms in a direction at 60∘C with the direction of motion of source, then the apparent frequency heard by observer is (speed of sound is 340ms)
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA turning fork vibrating at 500Hz falls from rest accelerates at 10m/s2.
Velocity of the tuning fork when waves with a frequency of 475Hz reach the release point is ( Take the speed of sound in air to be 340m/s).
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.
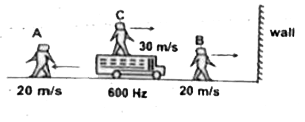
Find the frequency of direct sound observed by observer A
View SolutionThe frequency of a source of sound as measured by an observer when the source is moving towards him with a speed of 30 m/s is 720 Hz. The apparent frequency when the source is moving away after crossing the observer is x×102Hz what is the value of x. ......... (velocity of sound is 330 m/s)
View SolutionA source of sound which emitting a sound of frequency 600 Hz is moving towards a wall with a velocity 30 m/s. Three observes A, B, C moving with velocity 20 m/s, A away from the wall and B towards the wall and Inside the source, Velocity of sound in air is 330 m/s.

Find the frequency of reflected sound observed by observer B
View SolutionTwo tuning forks A and B having a frequency of 500 Hz each are placed with B to the right of A. An observer in between the forks in moving towards B with a speed of 25 m/s. The speed of sound is 345 m/s and the wind speed is 5 m/s from A to B. Calculate the difference in the two frequencies heard by observer.
View Solution
