A disposable galvanic cell is produced using of and of . It is needed to power a pace maker that draws a constant current of Amp to run it and requires atleast to function. Calculate the value of when cell reaches at .
(Given: .
The correct Answer is:1
To solve the problem, we need to calculate the concentration of Zn2+ when the cell reaches a voltage of 0.5V at 298K. We will use the Nernst equation and the given standard reduction potentials.
Step 1: Identify the half-reactions and standard potentials
The cell consists of two half-reactions:
- Anode (oxidation): Zn→Zn2++2e− with E∘=−0.76V
- Cathode (reduction): Sn2++2e−→Sn with E∘=−0.14V
Step 2: Calculate the standard cell potential E∘cell
Using the formula:
E∘cell=E∘cathode−E∘anode
Substituting the values:
E∘cell=(−0.14)−(−0.76)=0.62V
Step 3: Write the Nernst equation
The Nernst equation is given by:
Ecell=E∘cell−0.0591nlog((Zn2+)(Sn2+))
Where n is the number of moles of electrons transferred (which is 2 in this case).
Step 4: Set up the equation for the cell at 0.5V
We know:
- Ecell=0.5V
- E∘cell=0.62V
- The initial concentrations are (Zn2+)=0.5M and (Sn2+)=0.5M.
Substituting into the Nernst equation:
0.5=0.62−0.05912log((Zn2+)0.5)
Step 5: Rearranging the equation
Rearranging gives:
0.5−0.62=−0.02955log((Zn2+)0.5)
−0.12=−0.02955log((Zn2+)0.5)
Step 6: Solve for the logarithm
Dividing both sides by −0.02955:
log((Zn2+)0.5)=−0.12−0.02955≈4.06
Step 7: Exponentiate to find (Zn2+)
Taking the antilogarithm:
(Zn2+)0.5=104.06
(Zn2+)=0.5×104.06≈0.5×11513.56≈5756.78M
Conclusion
The concentration of Zn2+ when the cell reaches 0.5V is approximately 5756.78M.
---
The cell consists of two half-reactions:
- Anode (oxidation): Zn→Zn2++2e− with E∘=−0.76V
- Cathode (reduction): Sn2++2e−→Sn with E∘=−0.14V
Using the formula:
E∘cell=E∘cathode−E∘anode
Substituting the values:
E∘cell=(−0.14)−(−0.76)=0.62V
The Nernst equation is given by:
Ecell=E∘cell−0.0591nlog((Zn2+)(Sn2+))
Where n is the number of moles of electrons transferred (which is 2 in this case).
We know:
- Ecell=0.5V
- E∘cell=0.62V
- The initial concentrations are (Zn2+)=0.5M and (Sn2+)=0.5M.
0.5=0.62−0.05912log((Zn2+)0.5)
Rearranging gives:
0.5−0.62=−0.02955log((Zn2+)0.5)
−0.12=−0.02955log((Zn2+)0.5)
Dividing both sides by −0.02955:
log((Zn2+)0.5)=−0.12−0.02955≈4.06
Taking the antilogarithm:
(Zn2+)0.5=104.06
(Zn2+)=0.5×104.06≈0.5×11513.56≈5756.78M
The concentration of Zn2+ when the cell reaches 0.5V is approximately 5756.78M.
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - Part (II) EXERCISE-01
44 Videos
- ELECTROCHEMISTRYBOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - EXERCISE-02
35 Videos
- ELECTROCHEMISTRYBOOK - ALLENCHAPTER - ELECTROCHEMISTRYEXERCISE - COMPREHENSION TYPE
18 Videos
- CHEMISTRY AT A GLANCEBOOK - ALLENCHAPTER - CHEMISTRY AT A GLANCEEXERCISE - ORGANIC CHEMISTRY
472 Videos
- HYDROCARBONBOOK - ALLENCHAPTER - HYDROCARBONEXERCISE - MCQ
15 Videos
Similar Questions
Calculate Ecell at 25∘C for the reaction :
Zn+Cu2+(0.20M)→Zn2+(0.50M)+Cu
Given EΘ(Zn2+/Zn)=−0.76V,EΘ(Cu2+/Cu)=0.34V.
View SolutionCalculate the maximum work that can be obtained from the decimolar Daniell cell at 25∘C.
Given Ec−.(Zn2+∣Zn)=−0.76V and Ec−.(Cu2+∣Cu)=0.34V
View SolutionCalculate the equilibrium constant for the reaction at 298K.
Zn(s)+Cu2+(aq)⇔Zn2+(aq)+Cu(s)
Given, E∘Zn2+/Zn=−0.76V and E∘Cu2+/Cu=+0.34V
View SolutionCalculate the equilibrium constant for the reaction at 298K.
Zn(s)+Cu2+(aq)⇔Zn2+(aq)+Cu(s)
Given, E∘Zn2+/Zn=−0.76V and E∘Cu2+/Cu=+0.34V
View SolutionFor the given cell arrangement identify incorrect statement
given E∘_(Cu2+/Cu) = 0.34V &E∘_(Zn2+/Zn)=−0.76V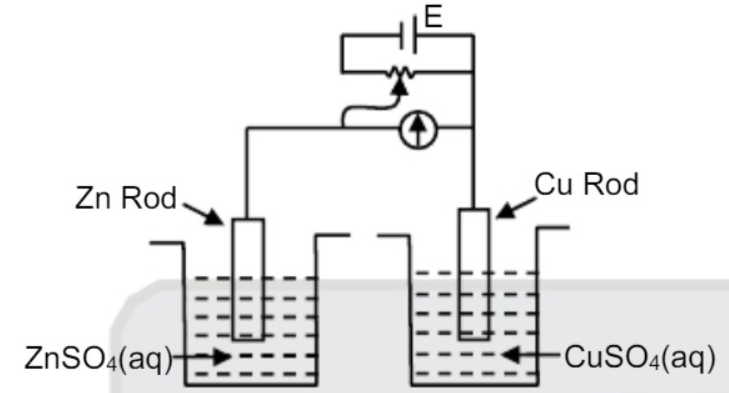
View SolutionConstruct a cell using given electrodes at 298K and also calculate its standart EMF.
Given : Ec−.Zn∣Zn2+=0.76V
Ec−.Cu2+∣Cu=0.34V
View SolutionCan a solution of 1 M ZnSO4 be stored in a vessel made of copper ? Given that
E∘Zn+2/Zn=−0.76VandE∘Cu+2/Cu=0.34V
View SolutionCalculate the e.m.f. of the cell
Zn/Zn2+(0.1M)||Cu2+(0.01M)|Cu
EΘZn2+/Zn=−0.76 V and EΘCu2+/Cu=0.34V
View SolutionWrite the cell reaction and calculate the e.m.f. of the following cell at 298 K :
Sn(s) ∣∣Sn2+(0.004M)∣∣∣∣H+(0.020M)∣∣H2(g) (1 bar )| Pt(s)
(Given E∘Sn2+/Sn=−0.14V).
View SolutionStandard reduction electrode potential of Zn2+/Zn is -0.76V. This means:
View Solution
