A charged particle having a mass of 1.6×10−26kg comes out of accelerator tube with kinetic energy 2×103eV . Calculate the smallest magnitude of the magnetic field that should be applied in vertically downwards direction to just prevent the charged particle from colliding the plate (Assume charge on particle = charge of the proton)
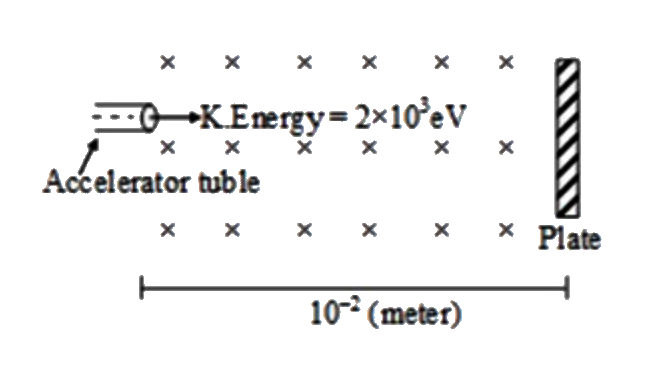
2 Tesla
4 Tesla
0.02 Tesla
0.04 Tesla
The correct Answer is:A
r=d or √2mkqB=d⇒B=√2mkq2d2
or B=√2×1.6×10−26×2×103×ee2×10−4
B=√2×1.6×10−26×2×1031.6×10−19×10−4=2 Tesla
Similar Questions
Knowledge Check
A particle is moving towards east enters in a magnetic field directed towards north and deflected in vertically downward direction. The charged particle is
Aan electronBa protonCan alpha particleDa neutronA charged particle of mass 0.003 g is held stationary in space by placing it in a downward direction of electric field of 6×104NC−1. Then, the magnitude of charge is
A5×10−4CB5×10−10CC5×10−6CD5×10−9CA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2t
A beam of charged particle, having kinetic energy 103eV, contains masses 8×10−27kgand1.6×10−26kg emerge from the end of an accelerator tube. There is a plate at distance 102m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionThe magnetic field is confirmed in a square region. A positive charged particle of charge q and mass m the limiting velocities of the particles so that it may come out of face (1), (2), (3), and (4).

View SolutionTwo charges particles each having equal charges 2×10−5C are brought from infinity to within a separation of 10 cm. Calculate the increase in potential energy during the process and the work required for this purpose.
View SolutionIf a particle moves in a circular path in clockwise direction after entering into a downward vertical magnetic field. The charge on the particle is-
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution