What is spherical capacitor?Derive expression for its capacitance.Solution in Punjabi
Spherical Capacitor : A capacitor which consists of two concentric spherical shells, out of which one is earthed and other is used to store charge, is known as a spherical capacitor
Capacitance of a spherical capacitor : Let we have a spherical capacitor.which consists of two spherical shells P and Q.
Let a = radius of spherical shell P
b = radius of spherical shell Q.
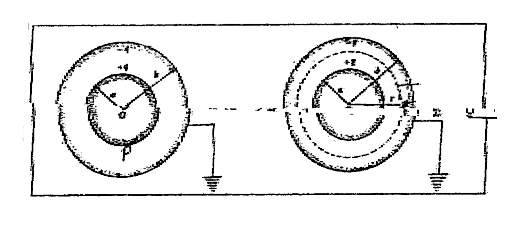
The outer spherical shell Q is connected to earth. When charge + q is given to inner spherical shell P. it induces charge - q on the inner surface of the shell Q and + q on its outer surface. As the shell Q is earthed, the charge + q on its outer surface flows to earth. If V is potential difference between the spherical shells P and Q.then capacitance of the spherical capacitor is given by
As the electric field between the two spherical shells is not uniform
(in magnitude)
and
The potential difference Fbetween the two spherical shells P and Q can be found by integrating both sides between the proper limits. Therefore,
To find the value of K, let us find electric field E at any point, say L between the two spherical shells. Let r be the distance of point L from the centre O of the spherical shells. Consider the dotted sphere of radius r through point L as the gaussian surface. The gaussian-surface encloses the spherical shell P and hence the charge enclosed by the gaussian surface is q. According to Gauss.s theorem, the total electric flux through the gaussian surface,
...........(1)
As the magnitude of electric field at every point on the gaussian surface is same, we have
surface area of gaussian surface
or .....(2)
From eqns. (1) and (2), we have
Put value of E in equation
Therefore, capacitance of the spherical capacitor is given by:
which is the required expression for the capacitance of a spherical capacitor.
Topper's Solved these Questions
- CAPACITANCE Book:BETTER CHOICE PUBLICATIONChapter:CAPACITANCE Exercise:NUMERICAL PROBLEMS
Explore 21 Videos
- CAPACITANCE Book:BETTER CHOICE PUBLICATIONChapter:CAPACITANCE Exercise:MOST EXPECTED NUMERICALS
Explore 5 Videos
- CAPACITANCE Book:BETTER CHOICE PUBLICATIONChapter:CAPACITANCE Exercise:SHORT ANSWER TYPE QUESTIONS (3/4 MARKS QUESTIONS)
Explore 11 Videos
- ALTERNATING CURRENTS Book:BETTER CHOICE PUBLICATIONChapter:ALTERNATING CURRENTS Exercise:MOST EXPECTED QUESTIONS
Explore 11 Videos
- CLASSIFICATION OF MATERIALSBook:BETTER CHOICE PUBLICATIONChapter:CLASSIFICATION OF MATERIALSExercise:Most expected question (2 marks)
Explore 3 Videos
Similar Questions
A parallel plate capacitor with air between the plates has a capacitance of 8 pF. The separation between the plates is now reduced by half and the space between them is filled with a medium of dielectric constant K. Calculate the value of the capacitance of the capacitor in the second case.
View SolutionConnect three capacitors of 3μF,3μF and 6μF such that their equivalent capacity becomes 5μF
View SolutionDerive an expression for energy density of a parallel plate capacitor.
View SolutionWhat is a phasor?
View SolutionDoes the magnetisation of a paramagnetic salt dependon temperature ? Give reason for your answer.
View SolutionWrite down the expression for the capacitance of a spherical capacitor.
View Solutionकिसी गोलीय संधारित्र की धारिता के लिए व्यंजक प्राप्त कीजिए ।
View Solutionसंधारित्र की धारिता की परिभाष लिखिए। समांतर-प्लेट संधारित्र की धारिता का व्यंजक व्युत्पादित कीजिए। इसकी धारिता कैसे बड़े जा सकती है?
View Solutionगोलीय संधारित्र की धारिता के लिए व्यंजक ज्ञात कीजिए | इसकी धारिता किन-किन बातो पर निर्भर करती है ?
View Solutionसंधारित्र किसे कहते हैं ? गोलीय संधारित्र की धारिता का व्यंजक व्युत्पन्न कीजिए । आवश्यक चित्र बनाइए।
View Solutionगोलीय संधारित्र की धारिता इसकी .............के समानुपाती होती है।
View Solutionबेलनाकार संधारित्र की धारिता का व्यंजक व्युत्पन्न करे।
View SolutionDerive an expression for the capacitance of a parallel plate capacitor. Explain the effect of dielectrics on capacitance of this capacitor. Or. Derive expression for capacitance of a parallel plate capacitor. Explain the effect of dielectrics on its capacitance.
View Solutionसंधारित्र किसे कहते हैं ? गोलीय संधारित्र की धारिता का व्यंजक व्युत्पन्न कीजिए धारिता बढ़ाने के उपाय लिखिए।
View Solutionगोलीय संधारित्र की धारिता के लिए व्यंजक ज्ञात कीजिये। इसकी धारिता कैसे बड़ाई जा सकती है ।
View SolutionWhat is a capacitor? Derive an expression for capacitance of a parallel plate capacitor.
View Solution