(0.8)4−(0.6)4(0.8)2+(0.6)2=?
0.28
0.36
0.64
0.24
The correct Answer is:A
Step by step video, text & image solution for ((0.8)^(4)-(0.6)^(4))/((0.8)^(2)+(0.6)^(2))=? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - MAHESH MISHRACHAPTER - सरलीकरण EXERCISE - 1 B. प्रतियोगी परीक्षाओं में पूछे गए प्रश्न176videos
सरलीकरण
- BOOK - MAHESH MISHRACHAPTER - समीकरणों की समानता EXERCISE - प्रतियोगी परीक्षाओ हेतु अभ्यास प्रश्नमाला27videos
समीकरणों की समानता
- BOOK - MAHESH MISHRACHAPTER - साझेदारी EXERCISE - 12 C प्रतियोगी परीक्षाओं हेतु अभ्यास प्रश्नमाला40videos
साझेदारी
Similar Questions
(0.03)2−(0.01)20.03−0.01=?
00:58View Solutionनीचे दिए गए प्रत्येक प्रश्न के 4 खंड है जिनमे से कोई 3 खंड के मान समतुल्य है। आपका उत्तर वह खंड है जिनके मान अन्य 3 के मान से भिन्न है।
01:12View Solutionरवि,प्रकाश और गंगाधर एक व्यापार की शुरूआत करते हैं तथा वे क्रमशः 27000 रु., 36000 रु.तथा 42000 रु.निवेश करते हैं । यदि वर्ष के अन्त में कुल 7000 रु.का लाभ हुआ हो, तो उसमें से गंगाधर का हिस्सा क्या होगा?
02:25View Solution(0.6)4−(0.5)4(0.6)2+(0.5)2 is equal to (a) 0.1 (b) 0.11 (c) 1.1 (d) 11
03:03View SolutionThe square root of 0.4 is 0.6 (b) 0.7 (c) 0.8 (d) 0.9
01:51View SolutionIf P (A) =0.8, P(B)=0.6, P(A∩B)=0.5, then P(B'|A')=
03:24View Solutionयादरच्या किसी परीक्षण में A और B दो घटनाएँ है ताकि P(A)=0.4P(B)=0.8 और P(B/A)=0.6 P(A//B)=
01:43View SolutionIf P(A)=0.8,P(B)=0.6andP(A∪B)=0.9,then P(A/B)andP(B/A) are respectively
02:07View SolutionIf P(A)=0.8,P(B)=0.6andP(A∩B)=0.5, then P(B'/A')=
00:44View SolutionIf A and B are two events such that P(A)=0.4,P(B)=0.8andP(B/A)=0.6, then P(¯¯¯A∩B) is
02:01View Solution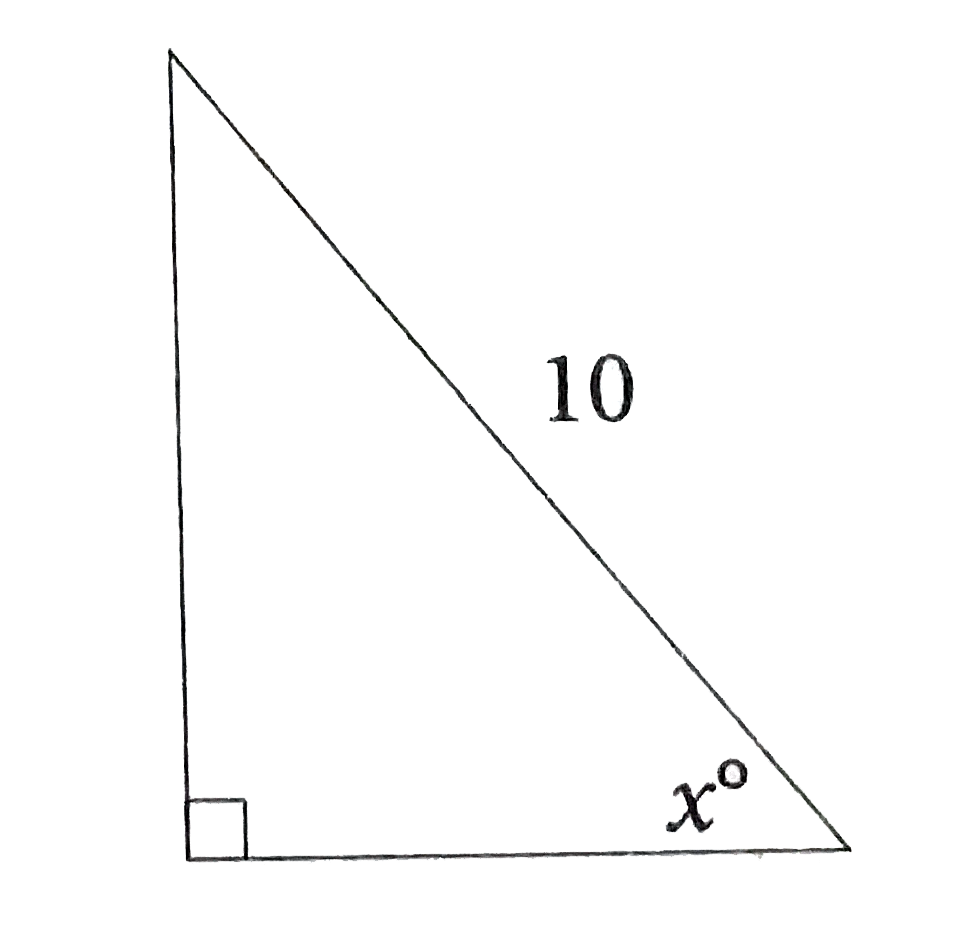
In the triangle above, sin x=0.8 and cos x=0.6. What is the area of the triangle?02:34View SolutionWhich is bigger, (34)2or(0.8)2?
01:05View SolutionIf A and B are two events such that P(A)=0.5,P(B)=0.6,P(A∪B)=0.8, find P(A|B).
02:59View Solutionयदि P(A) = 0.4, P(B) = 0.8 तथा P(BA)=0.6, तो P(A∪B) बराबर है :
05:31View SolutionA and B are two events such that P(A)= 0.8, P(B) = 0.6 and P (A∩B)=0.5, then the value of P(A/B) is
02:33View Solution(27)43+(32)0.8+(0.8)−1
02:29View Solution
