A body of 6 kg rests in limiting equilibrium on an inclined plane whose slope is 30∘. If the plane is raised to a slope of 60∘, the force in kg along the plane required to support it is
3 kg
2√3 kg
√3 kg
3√3 kg
The correct Answer is:B
To solve the problem, we need to determine the force required to support a 6 kg body on an inclined plane when the slope is raised from 30 degrees to 60 degrees. We will use the concepts of friction and the forces acting on the body.
1. Identify the Mass and Weight:
- Given mass m=6kg.
- Weight W=mg=6×10=60N.
2. Determine the Coefficient of Friction:
- The angle of repose at 30 degrees gives us the coefficient of friction μ.
- μ=tan(30∘)=1√3.
3. Analyze Forces on the Inclined Plane:
- When the plane is at 60 degrees, the forces acting on the body are:
- The weight component along the incline: W∥=mgsin(60∘).
- The normal force: N=mgcos(60∘).
- The frictional force opposing the motion: Ff=μN.
4. Calculate the Weight Components:
- Calculate W∥:
W∥=mgsin(60∘)=60×√32=30√3N
- Calculate the normal force N:
N=mgcos(60∘)=60×12=30N
5. Calculate the Frictional Force:
- Calculate the frictional force Ff:
Ff=μN=1√3×30=30√3=10√3N
6. Set Up the Equation for Equilibrium:
- For the body to be in equilibrium, the applied force F along the incline must balance the weight component down the incline minus the frictional force:
F+Ff=W∥
- Rearranging gives:
F=W∥−Ff=30√3−10√3=20√3N
7. Convert Force to kg:
- Since 1 N = 0.1 kg, we convert the force:
F=20√310=2√3kg
Final Answer:
The force required to support the body when the plane is raised to a slope of 60 degrees is 2√3kg.
- Given mass m=6kg.
- Weight W=mg=6×10=60N.
- The angle of repose at 30 degrees gives us the coefficient of friction μ.
- μ=tan(30∘)=1√3.
- When the plane is at 60 degrees, the forces acting on the body are:
- The weight component along the incline: W∥=mgsin(60∘).
- The normal force: N=mgcos(60∘).
- The frictional force opposing the motion: Ff=μN.
- Calculate W∥:
W∥=mgsin(60∘)=60×√32=30√3N
- Calculate the normal force N:
N=mgcos(60∘)=60×12=30N
- Calculate the frictional force Ff:
Ff=μN=1√3×30=30√3=10√3N
- For the body to be in equilibrium, the applied force F along the incline must balance the weight component down the incline minus the frictional force:
F+Ff=W∥
- Rearranging gives:
F=W∥−Ff=30√3−10√3=20√3N
- Since 1 N = 0.1 kg, we convert the force:
F=20√310=2√3kg
The force required to support the body when the plane is raised to a slope of 60 degrees is 2√3kg.
Similar Questions
A body of mass 4kg rests in limiting equilibrium on a rouch plane whose slope is 30∘. The slope is subsequently increased to 60∘. Calculate (i) coefficient of limiting friction between the body and the surface, (ii) acceleration down the plane if coefficient of kinetic friction is 0.4, (iii) force required to prevent it from sliding down the plane, (iv) force required to just move it up the plane. (g=9.8m/s2).
View SolutionA body of mass 2 kg slides down with an acceleration of 3 m/s2 on a rough inclined plane having a slope of 30∘ The external force required to take the same body up the plane with the same acceleration will be : (g=10m/s2)
View Solution
Knowledge Check
A block of 3kg rests in limiting equilibrium on an inclined plane of inclination 30∘. If the plane is raised to an inclination 60∘ , the force along the plane required to support it is
A10√3NB10√3NC10ND103NA block of 150kg is placed on an inclined plane withh an angle of 60∘. Calculate of the weight parallel to the inclined plane.
 A1300NB1400NC1100ND750N
A1300NB1400NC1100ND750NA rough inclined plane has its angle of inclination equal to 45∘ and μ=0.5. The magnitude of the least force in kg wt parallel to the plane required to move a body of 4 kg up the plane is
A3√2B2√2C√2D1/√2
A mass of 100kg is resting on a rough inclined plane of angle 30∘ If the coefficient of friction is 1/√3 find the greatest and the least forces that acting parallel to the plane in both cases just maintain the mass in equilibrium .
View SolutionA cylinder of mass m is kept on an inclined plane haivng an angle of inclination 30∘. Axis of the cylinder makes an angle 30∘ with the line along the greatest slope. Assuming that cylinder rolls without slipping, the acceleration of the cylinder is
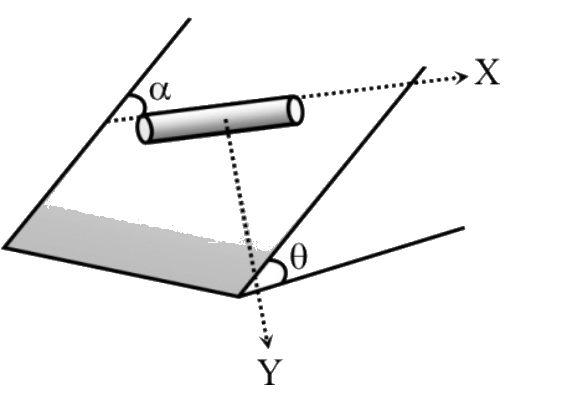
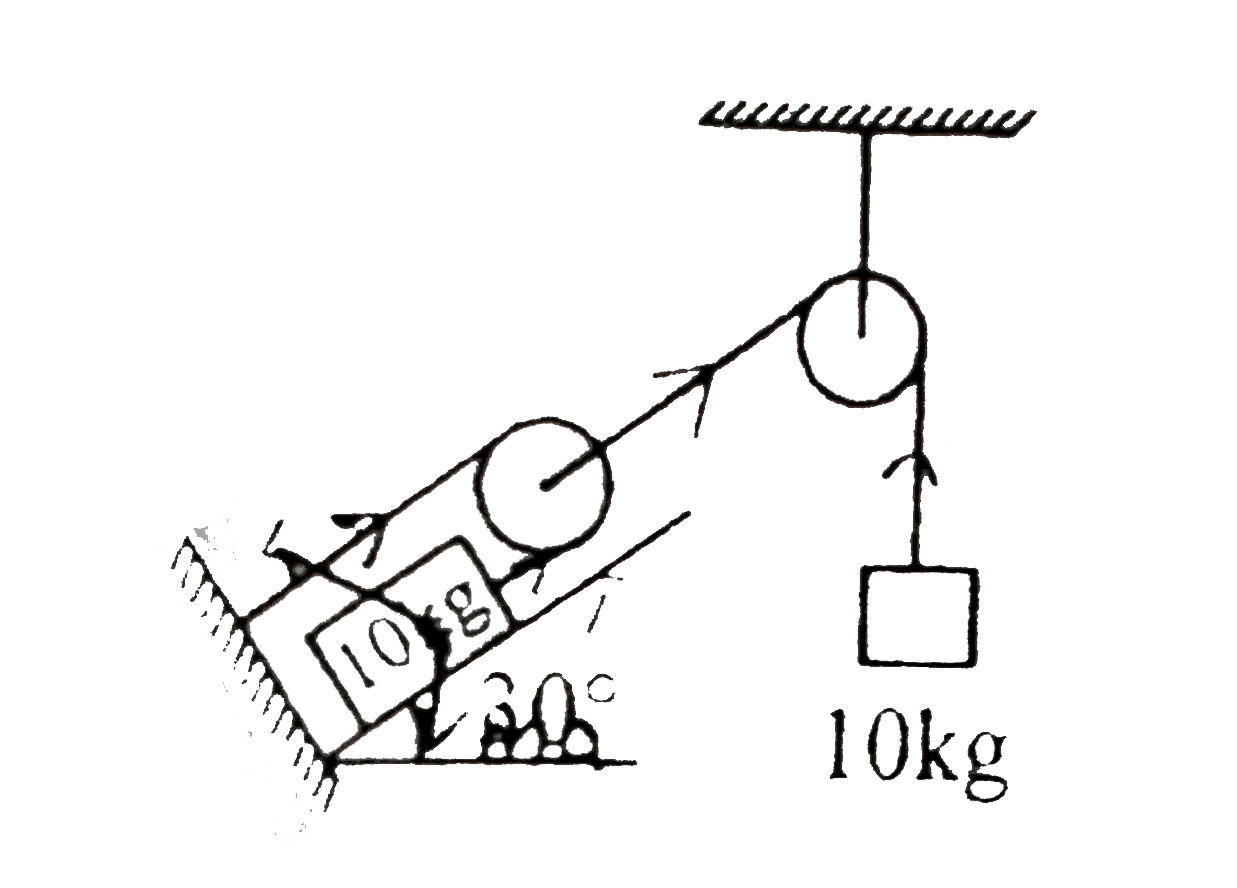
View SolutionThe acceleration of 10kg block on the inclined plane is
View SolutionA body of mass m=18kg is placed on an inclined plane the angle of inclination is α=37∘ and is attached to the top end of the slope with a thread which is parallel to the slope. Then the plane slope is moved with a horizontal acceleration of a. Friction is negligible.
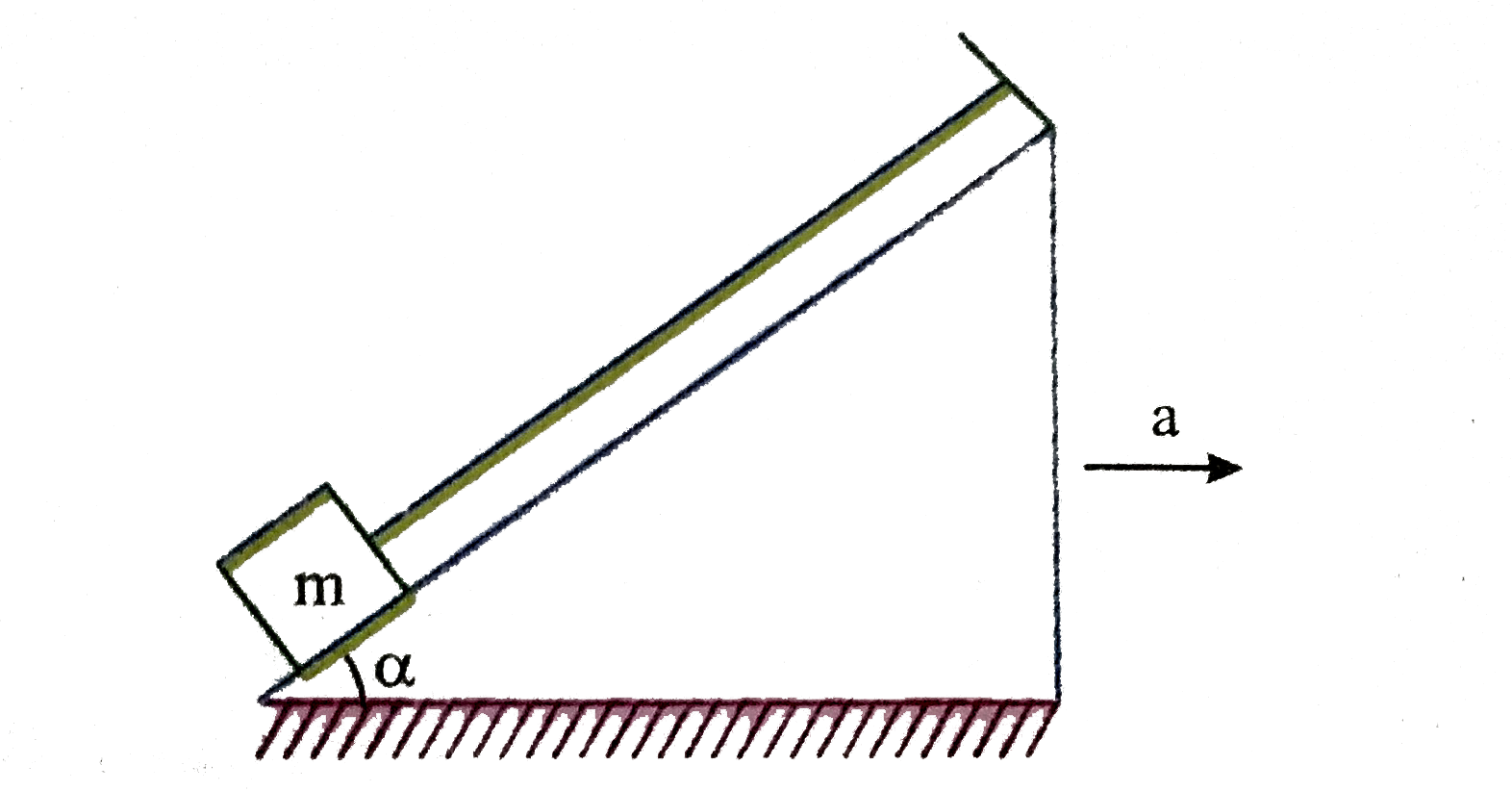
THe acceleration if the body pushes the plane with a force of 34mg is .
View SolutionA body of mass m=18kg is placed on an inclined plane the angle of inclination is α=37∘ and is attached to the top end of the slope with a thread which is parallel to the slope. Then the plane slope is moved with a horizontal acceleration of a. Friction is negligible.
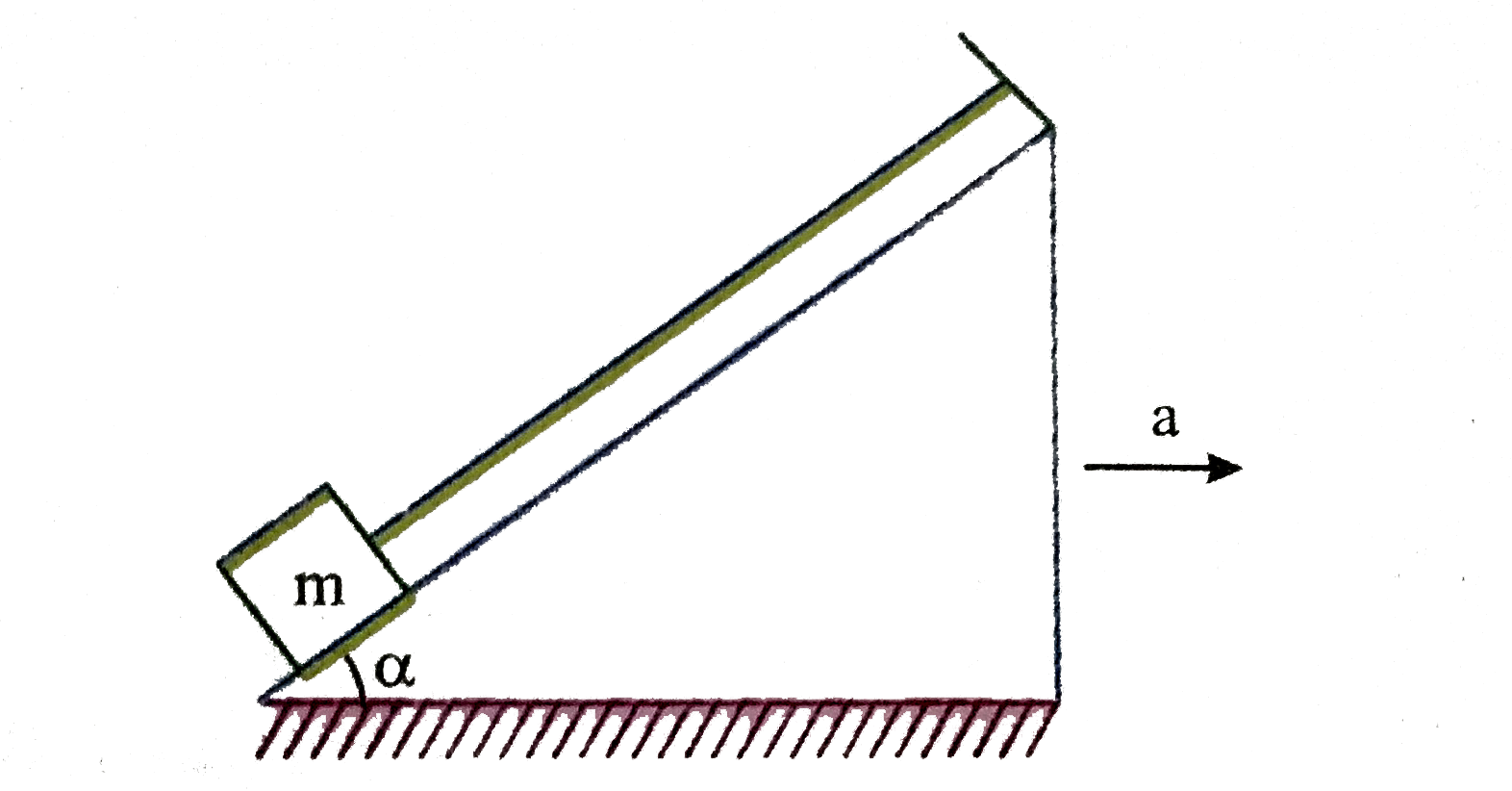
At what acceleration will the body lose contact with plane .
View Solution
