To ships 10 km apart on a line running south to north . The one father north is steaming west at 20 km/h. The other is steaming north at 20 km/h. The distance of closest approach is . . . . to reach it the time taken is . . . .
The correct Answer is:15 minutes , 5√2km
To solve the problem of finding the distance of closest approach and the time taken for two ships moving in different directions, we can follow these steps:
1. Understanding the Initial Setup:
- We have two ships: Ship A is 10 km south of Ship B.
- Ship A is moving west at a speed of 20 km/h.
- Ship B is moving north at a speed of 20 km/h.
2. Setting Up the Coordinate System:
- Let Ship B be at point (0, 10) (10 km north).
- Let Ship A be at point (0, 0) (0 km, at the origin).
- Ship A moves west, so its position at time t is given by (−20t,0).
- Ship B moves north, so its position at time t is given by (0,10+20t).
3. Finding the Distance Between the Ships:
- The distance d between the two ships at time t can be expressed using the distance formula:
d=√((−20t)−0)2+(0−(10+20t))2
- Simplifying this gives:
d=√(20t)2+(−(10+20t))2
=√400t2+(10+20t)2
=√400t2+(100+400t+400t2)
=√800t2+400t+100
4. Finding the Minimum Distance:
- To find the minimum distance, we need to minimize the function d2=800t2+400t+100.
- We can find the minimum by taking the derivative and setting it to zero:
d(d2)dt=1600t+400=0
1600t=−400⟹t=−14 (not valid as time cannot be negative)
- We need to check the critical points or use the second derivative test to find the minimum distance.
5. Using Geometry for Closest Approach:
- The closest distance can also be found geometrically. The ships are moving at right angles to each other.
- The closest approach occurs when the line connecting the two ships is perpendicular to their velocities.
- The distance of closest approach can be calculated using the right triangle formed by their paths:
Distance of closest approach=√(10)2+(20)2=√100+400=√500=10√5 km
6. Calculating the Time Taken:
- The relative velocity of the two ships can be calculated as:
vrel=√(20)2+(20)2=20√2 km/h
- The time taken to reach the closest approach can be calculated using:
t=DistanceRelative Velocity=10√520√2=√54√2 hours
Final Answers:
- Distance of Closest Approach: 10√5 km
- Time Taken: √54√2 hours
- We have two ships: Ship A is 10 km south of Ship B.
- Ship A is moving west at a speed of 20 km/h.
- Ship B is moving north at a speed of 20 km/h.
- Let Ship B be at point (0, 10) (10 km north).
- Let Ship A be at point (0, 0) (0 km, at the origin).
- Ship A moves west, so its position at time t is given by (−20t,0).
- Ship B moves north, so its position at time t is given by (0,10+20t).
- The distance d between the two ships at time t can be expressed using the distance formula:
d=√((−20t)−0)2+(0−(10+20t))2
- Simplifying this gives:
d=√(20t)2+(−(10+20t))2
=√400t2+(10+20t)2
=√400t2+(100+400t+400t2)
=√800t2+400t+100
- To find the minimum distance, we need to minimize the function d2=800t2+400t+100.
- We can find the minimum by taking the derivative and setting it to zero:
d(d2)dt=1600t+400=0
1600t=−400⟹t=−14 (not valid as time cannot be negative)
- We need to check the critical points or use the second derivative test to find the minimum distance.
- The closest distance can also be found geometrically. The ships are moving at right angles to each other.
- The closest approach occurs when the line connecting the two ships is perpendicular to their velocities.
- The distance of closest approach can be calculated using the right triangle formed by their paths:
Distance of closest approach=√(10)2+(20)2=√100+400=√500=10√5 km
- The relative velocity of the two ships can be calculated as:
vrel=√(20)2+(20)2=20√2 km/h
- The time taken to reach the closest approach can be calculated using:
t=DistanceRelative Velocity=10√520√2=√54√2 hours
- Distance of Closest Approach: 10√5 km
- Time Taken: √54√2 hours
Similar Questions
Two ships are 10km apart on a line joining south to north. The one farther north is steaming west at 20kmh−1. The other is steaming north at 20kmh−1. What their distance of closest approach ? How long do they take to reach itb ?
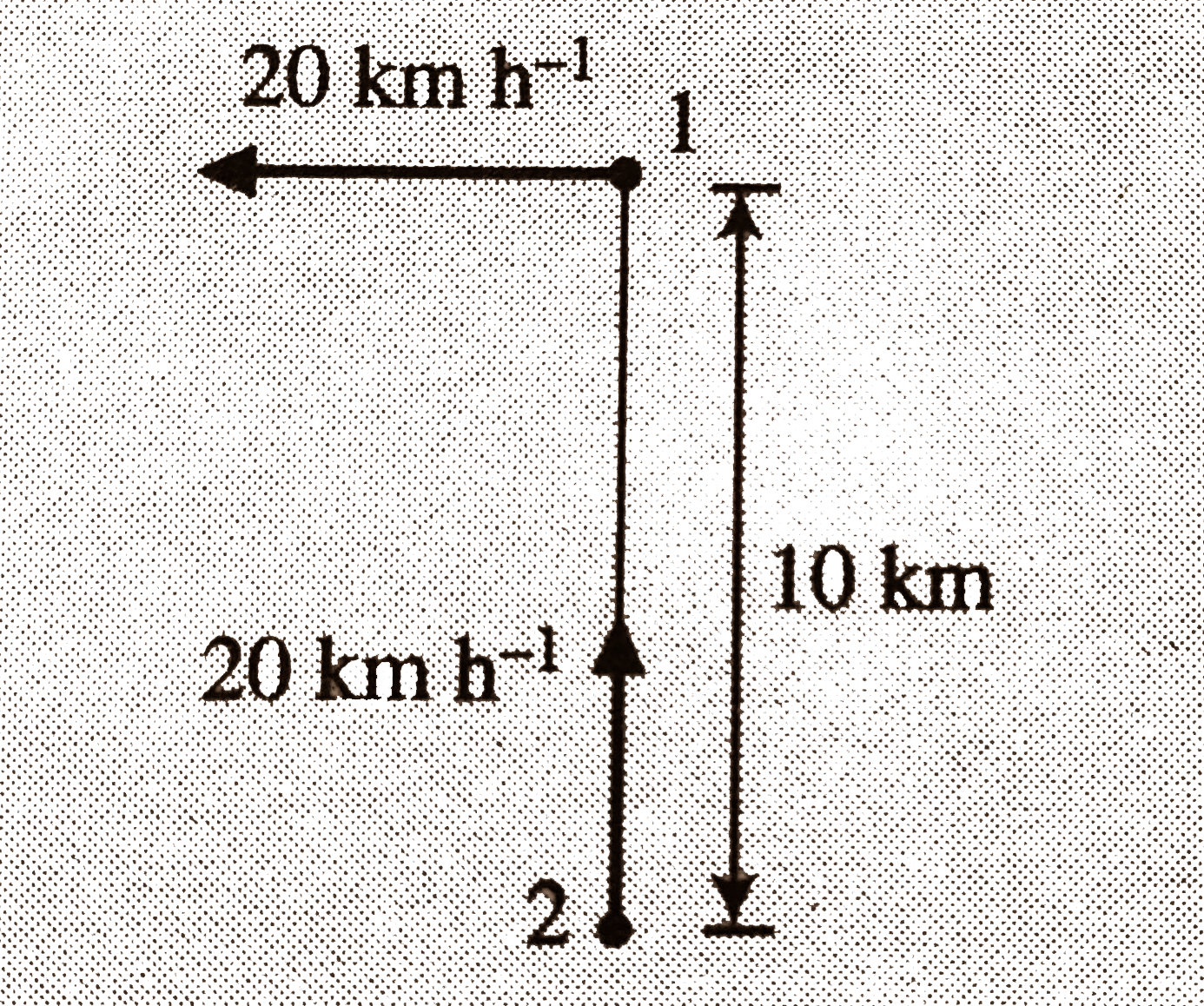 .
.
View SolutionTwo ships A and B are 10km apart on a line running south to north. Ship A farther north is streaming west at 20km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it?
View Solution
Knowledge Check
Two ships are 10km apart on a line from south to north.The one farther north is moving towards west at 40kmph and the other is moving towards north at 40kmph.Then distance of their closest approach is
A10kmB10√2kmC10√2kmD20kmTwo ships are 10√2 km apart on a line running south to north. The one further north is moving west with a speed of 25 km/h, while the other towards north with a speed of 25 km/h.
ATheir distance of closest approach is 5√2 km.BTheir distance of closest approach is 10 kmCTime required to reach the closest distance is 17 minDTime required to reach the closest distance is 29 min.A car A going north-east at 80km/h and another car B is going south-east at 60km/h. The direction of the velocity of A relative to B makes an angle with the north equal to:
Atan−1(2/7)Btan−1(7/2)Ctan−1(7)Dtan−1(1/7)
A plane is to fly due north. The speed of the plane relative to the air is 200 km/h, and the wind is blowing from west to east at 90 km/h.
View SolutionTwo boat A and B 20 km apart as shown. Boat a streaming east and boat B in north by 30km/hr then find shortest approach and time taken for it.

View SolutionAt a certain two cars area each 10km from the intersection of roads that are perpendiuclar. Cat A is moving east at 30 km/hr while car B moves north at 50km/hr both toward the intersection. (a) Fnd their closest distance of approach . (B) Where are A and B when they are closest?
View SolutionA runner runs 5 km north, then 8 km east and then 11 km south. How far is she from her starting point?
View SolutionA man is walking north with speed 4.5 km/h . Another is running west with speed 6 km/h . The velocity (mag. and direction ) of the second relative to the first is
View Solution
