A man wishes to cross a river to an exactly opposite point on the other bank. if the can swim with twice the velocity of the current, the inclination to the current of the direction he should swim is
30∘
45∘
60∘
120∘
The correct Answer is:D
To solve the problem of a man wishing to cross a river to an exactly opposite point on the other bank while swimming with a velocity that is twice that of the current, we can follow these steps:
Step 1: Define Variables
Let:
- vs = velocity of the swimmer
- vc = velocity of the current
- The swimmer's velocity is given as vs=2vc.
Step 2: Set Up the Problem
The swimmer needs to swim at an angle θ upstream to counteract the downstream current. The goal is to ensure that the resultant velocity of the swimmer has no downstream component, allowing him to reach the point directly across the river.
Step 3: Resolve Velocities
The swimmer's velocity can be resolved into two components:
1. A component perpendicular to the current (across the river): vscos(θ)
2. A component parallel to the current (against the current): vssin(θ)
Step 4: Equate the Components
To cross directly to the opposite point, the upstream component of the swimmer's velocity must equal the downstream velocity of the current:
vssin(θ)=vc
Step 5: Substitute the Swimmer's Velocity
Substituting vs=2vc into the equation:
2vcsin(θ)=vc
Step 6: Simplify the Equation
Dividing both sides by vc (assuming vc≠0):
2sin(θ)=1
Step 7: Solve for sin(θ)
sin(θ)=12
Step 8: Find the Angle θ
To find θ, we take the inverse sine:
θ=sin−1(12)=30∘
Conclusion
The inclination to the current of the direction he should swim is 30∘.
---
Let:
- vs = velocity of the swimmer
- vc = velocity of the current
- The swimmer's velocity is given as vs=2vc.
The swimmer needs to swim at an angle θ upstream to counteract the downstream current. The goal is to ensure that the resultant velocity of the swimmer has no downstream component, allowing him to reach the point directly across the river.
The swimmer's velocity can be resolved into two components:
1. A component perpendicular to the current (across the river): vscos(θ)
2. A component parallel to the current (against the current): vssin(θ)
To cross directly to the opposite point, the upstream component of the swimmer's velocity must equal the downstream velocity of the current:
vssin(θ)=vc
Substituting vs=2vc into the equation:
2vcsin(θ)=vc
Dividing both sides by vc (assuming vc≠0):
2sin(θ)=1
sin(θ)=12
To find θ, we take the inverse sine:
θ=sin−1(12)=30∘
The inclination to the current of the direction he should swim is 30∘.
Similar Questions
A swimmer wishes to reach directly opposite point on the other bank of a river,flowing with velocity 4√2ms.The swimmer can swim with 8ms in still water.The angle with the flow direction he should swim to reach the directly opposite point is (A)450 (B)900 (C)1350 (D)1500
View SolutionA river is flowing from west to east direction with velocity v. A swimmer standing at the south bank wants to cross the river in order to reach a point just in front of the starting point. If the swimmer can swim at a speed of u w.r.t. the river flow, the angle with the north direction, required to swim is equal to?
View Solution
Knowledge Check
A man can swim in still water at a speed of 6kmph and he has to cross the river and reach just opposite point on the other bank.If the river is flowing at a speed of 3kmph,and the width of the river is 2km, the time taken to cross the river is (in hours)
A227B2√27C23D2√45A man who can swin at the rate of 2 kmhr)(in still river) crosses a river to a point exactly opposite on the other bank by swimming in a direction of 120∘ to the flow of the water in the river. The velocity of the water current in kmhr is
A1B3C12D32A man wishes to cross a river flowing with velocity u swims at an angle θ with the river flow.If the man swims with speed vand if the width of the river is d, then the drift travelled by him is
A(u+vcosθ)dvsinθB(u−vcosθ)dvsinθC(u−vcosθ)dvcosθD(u+vcosθ)dvcosθ
A man swimming in a river from a point. A on one bank has to reach a point C on other bank, which is at a distance l from the point B, directly opposite to A on other bank. River width is d and the current velocity is u0. Find the minimum speed of swimmer relative to still water with which he should swim.
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionA man is boat intends to cross river from A. If he rows perpendicular to the banks then he takes t1 = 10 minutes to reach the other bank and he reaches point C at a distance l = 120 m down the stream from the point B which is exactly opposite to A on the other bank. If he heads at a certain angle α to the straight path AB against the current he will reach point B in t2 = 12.5 minutes.
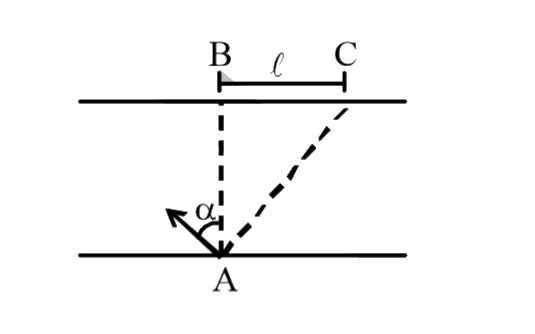
The width of river is-
View SolutionA man crosses a 320m wide river perpendicular to the current in 4 min. If in still water he can swim with a speed 5/3 times that of the current, then the speed of the current, in m/min is
View SolutionA man can swim with a certain speed, in still water to cross a river to a point directly opposite to the starting point in time t0. When the river flows, he crosses the river directly along the same path in a time t1, If 'd' be the river width, Then the velocity of water current is:
View Solution

