A firm manufactures two products A and B on which the profit earned per unit are Rs. 3 and Rs. 4 respectively. Each product is processed on two machines M1 and M2. Product A requires one minute of processing time on M1 and two minutes on M2 while B requires one minute on M1 and one minute on M2. Machine M1 is available for not more than 7 hours 30 minutes, while machine M2 is available for 10 hrs during any working day. Find the number of units of products A and B to manufactured to get maximum profit.
The correct Answer is:(0, 450), Rs. 1800
To solve the problem of maximizing profit from manufacturing products A and B, we can follow these steps:
Step 1: Define the Variables
Let:
- X = number of units of product A produced
- Y = number of units of product B produced
Step 2: Formulate the Objective Function
The profit earned per unit for product A is Rs. 3, and for product B is Rs. 4. Therefore, the total profit Z can be expressed as:
Z=3X+4Y
We want to maximize Z.
Step 3: Identify the Constraints
From the problem statement, we have the following constraints based on the processing time available on machines M1 and M2:
1. Machine M1:
- Each unit of A requires 1 minute and each unit of B requires 1 minute.
- Total available time for M1 is 7 hours 30 minutes = 450 minutes.
X+Y≤450
2. Machine M2:
- Each unit of A requires 2 minutes and each unit of B requires 1 minute.
- Total available time for M2 is 10 hours = 600 minutes.
2X+Y≤600
Step 4: Set Up the System of Inequalities
We can summarize the constraints as:
1. X+Y≤450
2. 2X+Y≤600
3. X≥0
4. Y≥0
Step 5: Graph the Constraints
To find the feasible region, we can graph the inequalities on a coordinate system where the x-axis represents product A (X) and the y-axis represents product B (Y).
1. For X+Y=450:
- When X=0, Y=450 (point A).
- When Y=0, X=450 (point B).
2. For 2X+Y=600:
- When X=0, Y=600 (point C).
- When Y=0, X=300 (point D).
Step 6: Identify the Corner Points
The feasible region is bounded by the lines and the axes. The corner points of the feasible region can be found by solving the equations:
1. Intersection of X+Y=450 and 2X+Y=600:
X+Y=450(1)
2X+Y=600(2)
Subtract (1) from (2):
2X+Y−(X+Y)=600−450
X=150
Substitute X=150 into (1):
150+Y=450⇒Y=300
So, one corner point is (150,300).
2. The other corner points are:
- (0,450) from X+Y=450
- (300,0) from 2X+Y=600
- (0,600) is not feasible since Y cannot exceed 450.
Step 7: Evaluate the Objective Function at Each Corner Point
Now we evaluate Z=3X+4Y at each corner point:
1. At (0,450):
Z=3(0)+4(450)=1800
2. At (150,300):
Z=3(150)+4(300)=450+1200=1650
3. At (300,0):
Z=3(300)+4(0)=900
Step 8: Determine the Maximum Profit
The maximum profit occurs at the point (0,450) with a profit of Rs. 1800.
Conclusion
To maximize profit, the firm should manufacture:
- 0 units of product A
- 450 units of product B
Let:
- X = number of units of product A produced
- Y = number of units of product B produced
The profit earned per unit for product A is Rs. 3, and for product B is Rs. 4. Therefore, the total profit Z can be expressed as:
Z=3X+4Y
We want to maximize Z.
From the problem statement, we have the following constraints based on the processing time available on machines M1 and M2:
- Each unit of A requires 1 minute and each unit of B requires 1 minute.
- Total available time for M1 is 7 hours 30 minutes = 450 minutes.
X+Y≤450
- Each unit of A requires 2 minutes and each unit of B requires 1 minute.
- Total available time for M2 is 10 hours = 600 minutes.
2X+Y≤600
We can summarize the constraints as:
1. X+Y≤450
2. 2X+Y≤600
3. X≥0
4. Y≥0
To find the feasible region, we can graph the inequalities on a coordinate system where the x-axis represents product A (X) and the y-axis represents product B (Y).
- When X=0, Y=450 (point A).
- When Y=0, X=450 (point B).
- When X=0, Y=600 (point C).
- When Y=0, X=300 (point D).
The feasible region is bounded by the lines and the axes. The corner points of the feasible region can be found by solving the equations:
1. Intersection of X+Y=450 and 2X+Y=600:
X+Y=450(1)
2X+Y=600(2)
Subtract (1) from (2):
2X+Y−(X+Y)=600−450
X=150
Substitute X=150 into (1):
150+Y=450⇒Y=300
So, one corner point is (150,300).
- (0,450) from X+Y=450
- (300,0) from 2X+Y=600
- (0,600) is not feasible since Y cannot exceed 450.
Now we evaluate Z=3X+4Y at each corner point:
1. At (0,450):
Z=3(0)+4(450)=1800
2. At (150,300):
Z=3(150)+4(300)=450+1200=1650
3. At (300,0):
Z=3(300)+4(0)=900
The maximum profit occurs at the point (0,450) with a profit of Rs. 1800.
To maximize profit, the firm should manufacture:
- 0 units of product A
- 450 units of product B
Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Fill in the blanks
9 Videos
- LINEAR PROGRAMMING BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Question
2 Videos
- LINEAR PROGRAMMING BOOK - ML KHANNACHAPTER - LINEAR PROGRAMMING EXERCISE - Self Assessment Test
8 Videos
- LIMITS, CONTINUITY AND DIFFERENTIABILITY BOOK - ML KHANNACHAPTER - LIMITS, CONTINUITY AND DIFFERENTIABILITY EXERCISE - MISCELLANEOUS EXERCISE (ASSERTION/ REASONS)
3 Videos
- LOGARITHMS AND SURDSBOOK - ML KHANNACHAPTER - LOGARITHMS AND SURDSEXERCISE - Miscellaneous exercise
3 Videos
Similar Questions
A firm manufactures two types of products, A and B, and sells them at a profit of Rs.5 per unit of type A and Rs.3 per unit of type B.Each product is processed on two machines, M1andM2. One unit of type A requires one minute of processing time on M1 and one minute on M2. Machines M1andM2. are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product the fiem should produce a day in order to maximize the profit. Solve the problem graphically.
View SolutionA firm manufactures two types of products, A and B, and sells them at a profil of 3 per unit to type B product and 5 perunit of type A product. Both product is processed on two machines M1and M2 One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2i whereas one unit of type B requires one minute of processing time on M1 and one minute on M Machines sells them at a profit of 5 per unit of type A and M, and M, are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product the firn should produce a day in order to maximize the profit. Solve the problem graphically [CHSE 2000]
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionA company manufacturers two types of products P and Q. The product P requires 5 minutes each for cutting and 10 minutes each for assembling. The product Q requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes availabe for cutting and 4 hours for assembling. The profit is 50 paise each for type P and 60 paise each for type Q. How many products of each type should the company manufacture in order to maximize the profit?
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package on screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacturer a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day order to maximise his profit? Determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA manufacturer makes two models A and B of a product. Each model is processed by two machines. To complete one unit of model. A, machines I and II must work 1 hours and 3 hours respectively. To complete one unit of model B, machine I and II must work 2 hours and 1 hour respectively. Machine I may not operate for more than 8 hours per day, and machine II for not more than 9 hours per day. If profits on model A and B per unit are Rs. 300 and Rs. 350, then how many units of each model should be produced , per day, to maximize the profits ?
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
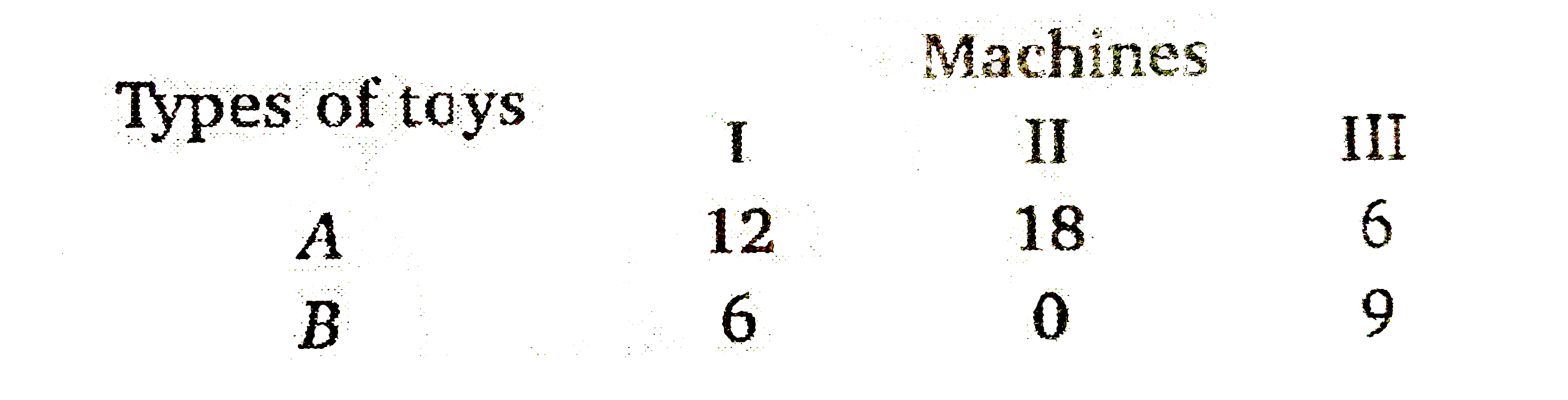
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5. show that 15 toys of type A and 30 of the B should be manufactured m a day to get maximum profit.
View Solution
