There are three works,one consisting of 3 volumes, one of 4, and the other of 1 volume. They are placed on a shelf at random. Find the chance that volumes of the same works are all together.
The correct Answer is:
To solve the problem step by step, we need to find the probability that the volumes of the same works are all together when placed on a shelf.
Step 1: Identify the total number of volumes
We have three works:
- Work 1: 3 volumes
- Work 2: 4 volumes
- Work 3: 1 volume
Total volumes = 3 + 4 + 1 = 8 volumes.
Step 2: Calculate the total arrangements of the volumes
The total arrangements of 8 volumes can be calculated using the factorial of the total number of volumes:
Total arrangements=8!=40320
Step 3: Group the volumes of the same work together
To find the arrangements where volumes of the same work are together, we can treat each work as a single unit or block:
- Block for Work 1 (3 volumes)
- Block for Work 2 (4 volumes)
- Block for Work 3 (1 volume)
Now we have 3 blocks to arrange:
- Total blocks = 3!
Step 4: Calculate the arrangements within each block
Now we need to arrange the volumes within each block:
- Work 1 (3 volumes): can be arranged in 3! ways.
- Work 2 (4 volumes): can be arranged in 4! ways.
- Work 3 (1 volume): can be arranged in 1! way.
Step 5: Calculate the total arrangements with blocks
The total arrangements where the volumes of the same work are together can be calculated as:
Arrangements with blocks=3!×3!×4!×1!
Calculating this:
3!=6,4!=24,1!=1
So,
Arrangements with blocks=3!×3!×4!×1!=6×24×1=144
Step 6: Calculate the probability
Now, we can find the probability that the volumes of the same works are all together:
Probability=Arrangements with blocksTotal arrangements=14440320
Step 7: Simplify the probability
To simplify:
14440320=1280
Final Answer
The probability that the volumes of the same works are all together is 1280.
We have three works:
- Work 1: 3 volumes
- Work 2: 4 volumes
- Work 3: 1 volume
The total arrangements of 8 volumes can be calculated using the factorial of the total number of volumes:
Total arrangements=8!=40320
To find the arrangements where volumes of the same work are together, we can treat each work as a single unit or block:
- Block for Work 1 (3 volumes)
- Block for Work 2 (4 volumes)
- Block for Work 3 (1 volume)
- Total blocks = 3!
Now we need to arrange the volumes within each block:
- Work 1 (3 volumes): can be arranged in 3! ways.
- Work 2 (4 volumes): can be arranged in 4! ways.
- Work 3 (1 volume): can be arranged in 1! way.
The total arrangements where the volumes of the same work are together can be calculated as:
Arrangements with blocks=3!×3!×4!×1!
Calculating this:
3!=6,4!=24,1!=1
So,
Arrangements with blocks=3!×3!×4!×1!=6×24×1=144
Now, we can find the probability that the volumes of the same works are all together:
Probability=Arrangements with blocksTotal arrangements=14440320
To simplify:
14440320=1280
The probability that the volumes of the same works are all together is 1280.
Topper's Solved these Questions
- PROBABILITYBook:ML KHANNAChapter:PROBABILITYExercise:MISCELLANEOUS EXERCISE (Comprehension)
Explore 1 Video
- PROBABILITYBook:ML KHANNAChapter:PROBABILITYExercise:MISCELLANEOUS EXERCISE (Assertion / Reason)
Explore 1 Video
- PROBABILITYBook:ML KHANNAChapter:PROBABILITYExercise:Problem Set (1) FILL IN THE BLANKS
Explore 17 Videos
- PERMUTATIONS AND COMBINATIONS Book:ML KHANNAChapter:PERMUTATIONS AND COMBINATIONS Exercise:SELF ASSESSMENT TEST
Explore 20 Videos
- PROGRESSIONS Book:ML KHANNAChapter:PROGRESSIONS Exercise:MISCELLANEOUS EXERCISE (ASSERTION/REASON)
Explore 1 Video
Similar Questions
There are two works each of 3 volumes and two works each of 2 volumes; In how many ways can be 10 books be placed on a shelf so that the volumes of the same work are not separated
View SolutionThere are two works each of 3 volumes and two works each of 2 volumes; In how many ways can the 10 books be placed on a shelf so that the volumes of the same work are not separated?
View Solution
Knowledge Check
There are 3 works. One is of 3 volumes, one is of 4 volumes and one is of only one and they are placed a random in at shelf. What is the chance that volume of the same work is placed together
A1/40B3/140C9/70DnoneThere are 3 works. One is of 3 volumes and one is of 4 volumes and one is of exactly one volume. If the books are placed in a random order on a shelf, the probability that all the volumes of the same work are together is
A170B3140C165D3130Eleven books consisting of 5 mathematics, 4 physics and 2 on chemistry are placed on a shelf at random. The number of possible ways of arranging them on the assumption that the books on the same subject are all together is
A4!.2!B11!C5!4!2!3!Dnone of these
A shelf contain 20 different books of which 4 are in single volume and the others form sets of 8,5 and 3 volumes respectively. Number of ways in which the books may be arranged on the shelf, if the volume of each set are together and in their due order
View Solution5 different Engineering, 4 different Mathematics and2 different Chemistry books are placed in a shelf at random. The probability that the books of each kind are all together is
View Solution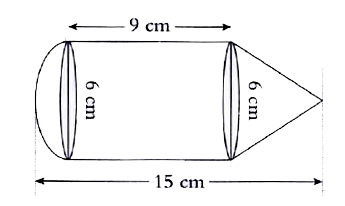
In the above figure , a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other . Find the volume of the solid .
View SolutionA shelf contains 20 books of which 4 are single volume and the other form sets of 8, 5, and 3 volumes. Find the number of ways in which the books (i)may be arranged on the shelf so that (ii)volumes of each set will not be separated. (iii)volumes of each set remain in their due order.
View SolutionThe explosion of a mixture consisting of one volume of a gas being studied and one volume of H2 yielded one volume of water vapour and one volume of N2, the volumes being measured under identical conditions. Find the formula of the gas being studied.
View Solution

