The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as (l1,m1,n1),(l2,m2,n2),(l3,m3,n3) are
l1+l2+l3,m1+m2+m3,n1+n2+n3
l1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3
l1+l2+l33,m1+m2+m33,n1+n2+n33
none of these
The correct Answer is:B
To find the direction cosines of a line that equally inclines to three mutually perpendicular lines, we can follow these steps:
Step 1: Understand the Direction Cosines
The direction cosines of a line are represented as (l,m,n). For three mutually perpendicular lines with direction cosines (l1,m1,n1), (l2,m2,n2), and (l3,m3,n3), we know that the following conditions hold:
1. l21+m21+n21=1
2. l22+m22+n22=1
3. l23+m23+n23=1
4. The dot products of the direction cosines of any two lines are zero:
- l1l2+m1m2+n1n2=0
- l2l3+m2m3+n2n3=0
- l1l3+m1m3+n1n3=0
Step 2: Set Up the Equations
Since the line is equally inclined to the three mutually perpendicular lines, we can express the conditions mathematically. The line's direction cosines (l,m,n) must satisfy:
- l=m=n
Step 3: Use the Condition of Equally Inclined
Since the line is equally inclined to the three lines, we can use the fact that the direction cosines can be expressed as:
l2+m2+n2=1
Substituting l=m=n gives:
3l2=1⟹l2=13⟹l=±1√3
Thus, we have:
l=m=n=1√3 or −1√3
Step 4: Conclusion
The direction cosines of the line that equally inclines to the three mutually perpendicular lines are:
(1√3,1√3,1√3) or (−1√3,−1√3,−1√3)
The direction cosines of a line are represented as (l,m,n). For three mutually perpendicular lines with direction cosines (l1,m1,n1), (l2,m2,n2), and (l3,m3,n3), we know that the following conditions hold:
1. l21+m21+n21=1
2. l22+m22+n22=1
3. l23+m23+n23=1
4. The dot products of the direction cosines of any two lines are zero:
- l1l2+m1m2+n1n2=0
- l2l3+m2m3+n2n3=0
- l1l3+m1m3+n1n3=0
Since the line is equally inclined to the three mutually perpendicular lines, we can express the conditions mathematically. The line's direction cosines (l,m,n) must satisfy:
- l=m=n
Since the line is equally inclined to the three lines, we can use the fact that the direction cosines can be expressed as:
l2+m2+n2=1
Substituting l=m=n gives:
3l2=1⟹l2=13⟹l=±1√3
Thus, we have:
l=m=n=1√3 or −1√3
The direction cosines of the line that equally inclines to the three mutually perpendicular lines are:
(1√3,1√3,1√3) or (−1√3,−1√3,−1√3)
Topper's Solved these Questions
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - PROBLEM SET (4)
19 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - MISCELLANEOUS EXERCISE(TRUE AND FALSE)
27 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - PROBLEM SET (2)
12 Videos
- BINOMIAL THEOREM AND MATHEMATICAL INDUCTION BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Self Assessment Test
35 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Assertion / Reason
2 Videos
Similar Questions
Knowledge Check
The direction cosines of a line equally inclines to three mutually perpendicular lines having D.C.'s
as (l1,m1,n1),(l2,m2,n2),(l3,m3,n3) areAthe direction cosines of three mutually perpendicular linesBthe direction ratios of three mutually perpendicular lines which are not direction cosines.Cthe direction cosines of three lines which need not be perpendicularDthe direction of three lines which need not be perpendicularThe direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as l1,m1,n1,l2,m2,n2 and l3,m3,n3 are
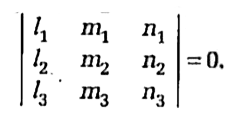
Al1+l2+l3,m1+m2+m3,n1+n2+n3Bl1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3Cl1+l2+l33,m1+m2+m33,n1+n2+n33Dnone of theseIf l1,m1,n1,l2,m2,n2andl3,m3,n3 are direction cosines of three mutuallyy perpendicular lines then, the value of ∣∣ ∣∣l1m1n1l2m2n2l3m3n3∣∣ ∣∣ is
Al3m3n3B±1Cl1m1n1Dl2m2n2
If three mutually perpendicular lines have direction cosines (l1,m1,n1),(l2,m2,n2)and(L3,m3,n3), then the line having direction cosines l1+l2+l3,m1+m2+m3,andn1+n2+n3, make an angle of
View SolutionThe direction cosines of a line bisecting the angle between two perpendicular lines whose direction cosines are l1,m1,n1 and l2,m2,n2 are (1)l1+l22,m1+m22,n1+n22 (2)l1+l2,m1+m2,n1+n2 (3)l1+l2√2,m1−m22,n1+n2√2 (4)l1−l2,m1−m2,n1−n2 (5)n o n eo ft h e s e
View SolutionLet li,mi,ni;i=1,2,3 be the direction cosines of three mutually perpendicular lines referred to an orthogonal cartesian co–ordinate system, then prove that A=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦is an orthogonal matrix.
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are
View Solution(l1,m1,n1),(l2,m2,n2),(l3,m3,n3) are the direction cosines of three mutually perpendicular lines. If the line, whose direction ratios are l1+l2+l3,m1+m2+m3,n1+n2+n3, makes angle θ with any of these three lines, then cosθ is equal to
View Solution