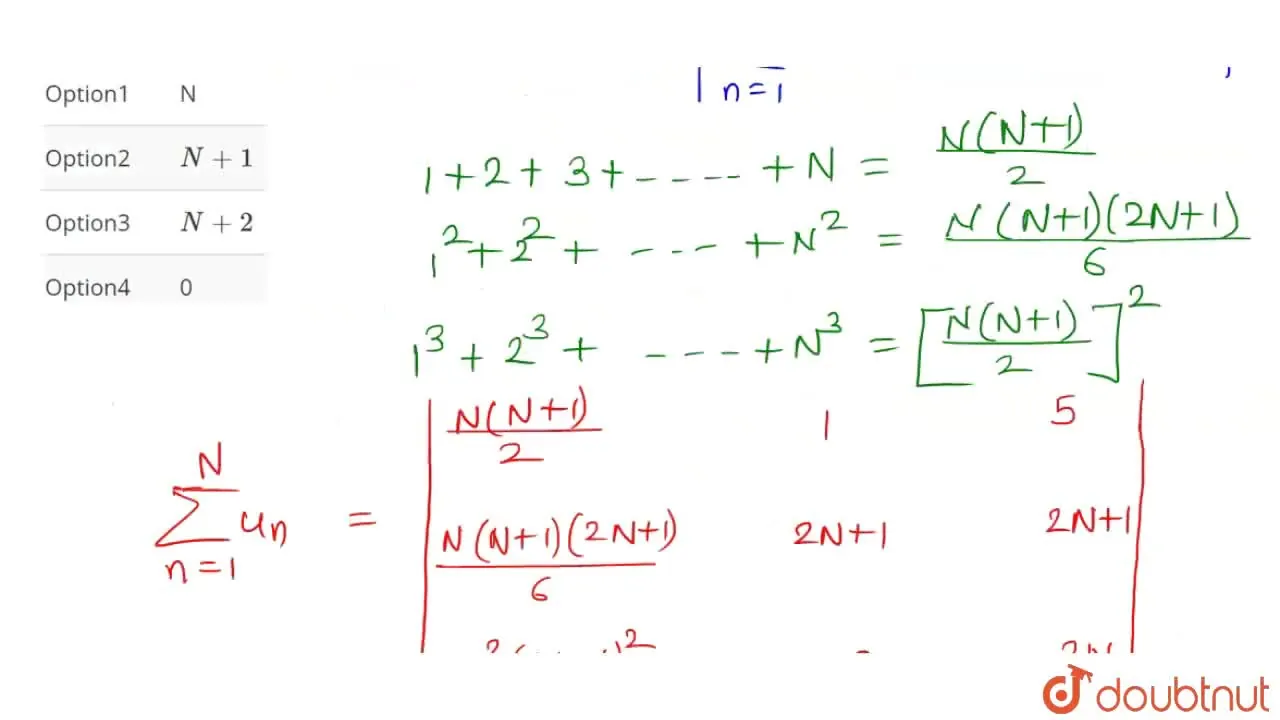If Un=∣∣ ∣ ∣∣n15n22N+12N+1n33N23N∣∣ ∣ ∣∣ then N∑n=1Un=
N
N+1
N+2
0
The correct Answer is:D
Step by step video, text & image solution for If U_n=|(n,1,5),(n^2,2N+1,2N+1),(n^3,3N^2,3N)| then sum_(n=1)^(N)U_n= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ML KHANNACHAPTER - DETERMINANTS EXERCISE - Problem Set (1) (TRUE AND FALSE)7videos
DETERMINANTS
- BOOK - ML KHANNACHAPTER - DETERMINANTS EXERCISE - Problem Set (2) (MULTIPLE CHOICE QUESTIONS)21videos
DETERMINANTS
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)1videos
DEFINITE INTEGRAL
- BOOK - ML KHANNACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - MISCELLANEOUS EXERCISE (Matching Entries)2videos
DIFFERENTIAL EQUATIONS
Similar Questions
If Un=∣∣ ∣ ∣∣n15n22N+12N+1n33N23N+1∣∣ ∣ ∣∣, then N∑n=1Un is equal to (A) 2N∑n=1n (B) 2N∑n=1(n2) (C) (12)N∑n=1(n2) (D) 0
View SolutionThe value of n∑n=1Un IfUn=∣∣ ∣ ∣∣n15n22N+12N+1n33N23N∣∣ ∣ ∣∣,is
View SolutionIf Un=∣∣ ∣ ∣∣n158n2359n32510∣∣ ∣ ∣∣ then 5∑n=1Un=
View SolutionIf Δk=∣∣ ∣ ∣∣k15k22n+12n+1k33n23n+1∣∣ ∣ ∣∣, then n∑k=1Δk is equal to
View SolutionIf Δa=∣∣ ∣ ∣∣a−1n6(a−1)22n24n−2(a−1)33n33n2−3n∣∣ ∣ ∣∣ then n∑a=1Δa in equal to
View SolutionLet Δa=∣∣ ∣ ∣∣(a−1)n6(a−1)22n24n−2(a−1)33n33n2−3n∣∣ ∣ ∣∣ the value of n∑a=1Δa is
View SolutionIf Sn=n∑n=12n+1n4+2n3+n2 then S10 is less then
View SolutionIf Un=1n−1n+1 , then the value of U1+U2+U3+U4+U5 is
View SolutionIf Un=1n−1n+1 , then the value of U1+U2+U3+U4+U5 is
View SolutionLet Un=n!(n+2)! where n∈N. If Sn=n∑n=1Un, then limn→∞Sn, equals
View Solution