The region represented by the inequality 2<|z+i|≤3 is . . . .
The correct Answer is:r1=2andr2=3
To solve the inequality 2<|z+i|≤3, we will break it down into two parts and analyze each part step by step.
Step 1: Rewrite the Complex Number
Let z=x+iy, where x and y are real numbers. The expression z+i can be rewritten as:
z+i=x+iy+i=x+i(y+1)
Step 2: Express the Modulus
The modulus |z+i| is given by:
|z+i|=|x+i(y+1)|=√x2+(y+1)2
Step 3: Analyze the First Part of the Inequality
The first part of the inequality is:
2<|z+i|
This implies:
2<√x2+(y+1)2
Squaring both sides gives:
4<x2+(y+1)2
This can be rewritten as:
x2+(y+1)2>4
This represents the region outside a circle centered at (0,−1) with a radius of 2.
Step 4: Analyze the Second Part of the Inequality
The second part of the inequality is:
|z+i|≤3
This implies:
√x2+(y+1)2≤3
Squaring both sides gives:
x2+(y+1)2≤9
This represents the region inside or on the boundary of a circle centered at (0,−1) with a radius of 3.
Step 5: Combine the Results
The combined inequalities are:
4<x2+(y+1)2≤9
This describes the annular region (ring-shaped area) between the two circles:
- The outer circle has a radius of 3.
- The inner circle has a radius of 2.
Conclusion
Thus, the region represented by the inequality 2<|z+i|≤3 is the area between the two circles centered at (0,−1) with radii 2 and 3, where the boundary of the outer circle is included, and the boundary of the inner circle is excluded.
---
Let z=x+iy, where x and y are real numbers. The expression z+i can be rewritten as:
z+i=x+iy+i=x+i(y+1)
The modulus |z+i| is given by:
|z+i|=|x+i(y+1)|=√x2+(y+1)2
The first part of the inequality is:
2<|z+i|
This implies:
2<√x2+(y+1)2
Squaring both sides gives:
4<x2+(y+1)2
This can be rewritten as:
x2+(y+1)2>4
This represents the region outside a circle centered at (0,−1) with a radius of 2.
The second part of the inequality is:
|z+i|≤3
This implies:
√x2+(y+1)2≤3
Squaring both sides gives:
x2+(y+1)2≤9
This represents the region inside or on the boundary of a circle centered at (0,−1) with a radius of 3.
The combined inequalities are:
4<x2+(y+1)2≤9
This describes the annular region (ring-shaped area) between the two circles:
- The outer circle has a radius of 3.
- The inner circle has a radius of 2.
Thus, the region represented by the inequality 2<|z+i|≤3 is the area between the two circles centered at (0,−1) with radii 2 and 3, where the boundary of the outer circle is included, and the boundary of the inner circle is excluded.
Topper's Solved these Questions
- COMPLEX NUMBERS Book:ML KHANNAChapter:COMPLEX NUMBERS Exercise:Problem Set (4) M.C.Q
Explore 26 Videos
- COMPLEX NUMBERS Book:ML KHANNAChapter:COMPLEX NUMBERS Exercise:Problem Set (4) (True and False)
Explore 4 Videos
- COMPLEX NUMBERS Book:ML KHANNAChapter:COMPLEX NUMBERS Exercise:Problem Set (3) (M.C.Q) Inequalities:
Explore 27 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBook:ML KHANNAChapter:CO-ORDINATE GEOMETRY OF THREE DIMENSIONExercise:SELF ASSIGNMENT TEST
Explore 11 Videos
- CONCEPTS OF SET THEORY Book:ML KHANNAChapter:CONCEPTS OF SET THEORY Exercise:Self Assessment Test
Explore 13 Videos
Similar Questions
Knowledge Check
The shaded region is represented by the inequality:
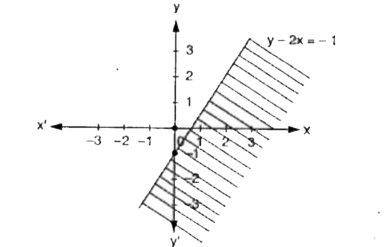 Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1
Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1The shaded region is represented by the inequation:
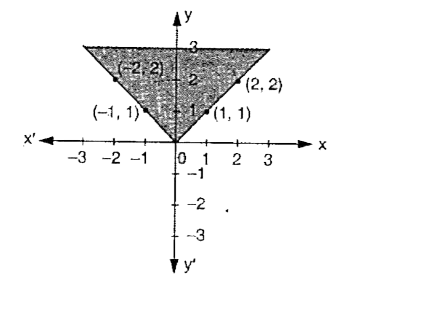 Ay≥xBy≥−xCy≥|x|Dy≤|x|
Ay≥xBy≥−xCy≥|x|Dy≤|x|Region represented by the inequalities x≥0,y≥0 is
Afirst quadrantBsecond quadrantCthird quadrantDfourth quadrant
Construct the region represented by the inequations x+y≥4and3x+2y≤6.
View SolutionConstruct the region represented by the inequation x+3y≥3and3x+y≤3
View SolutionThe region represented by inequalities arg(z)≤π3;|z|≤2;Im(z)≥1 in the argand diagram is given by
View SolutionThe total number of integral points i.e. points having integral coordinates lying in the region represented by the inequations |x−y|<3 and |x+y|<3 is
View SolutionThe region rprsented by the inequation system x,y≥0,y≤6,x+y≤3, is
View Solution

