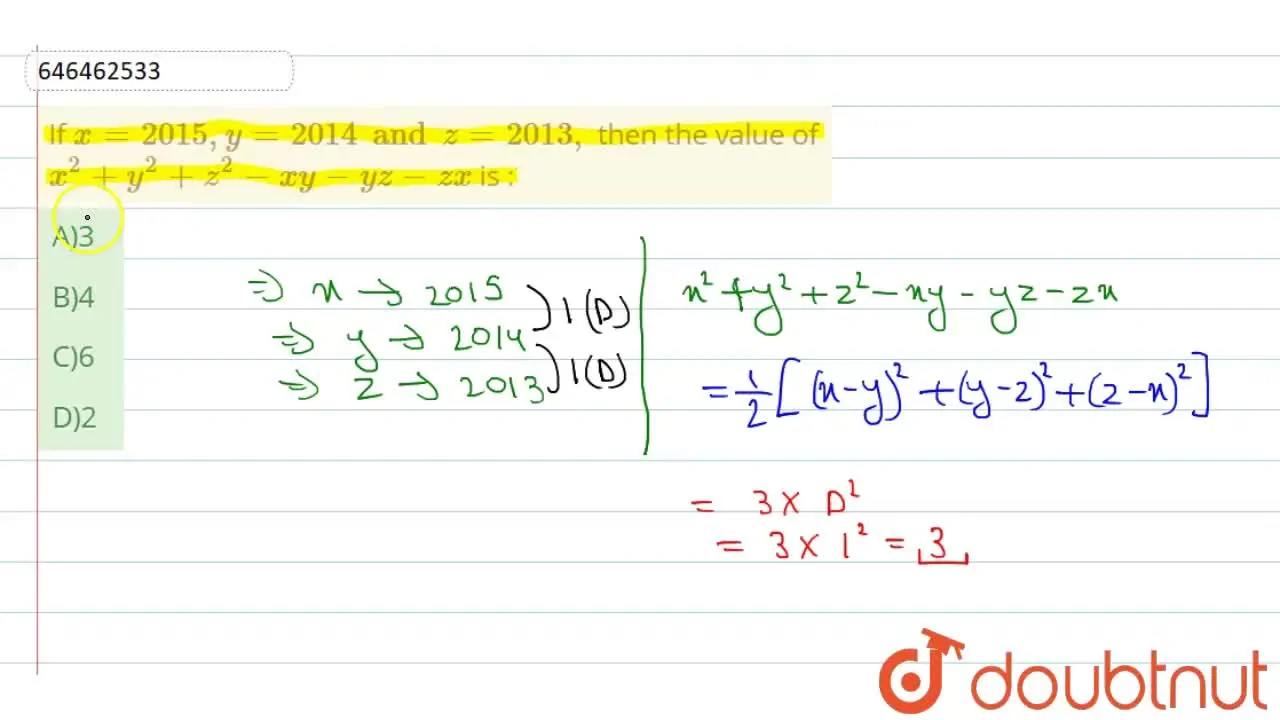
If x=2015,y=2014andz=2013, then the value of x2+y2+z2−xy−yz−zx is :
A)3
B)4
C)6
D)2
The correct Answer is:A
Step by step video, text & image solution for If x = 2015 , y = 2014 and z = 2013, then the value of x ^(2) + y^(2) + z ^(2) - xy - yz - zx is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
Similar Questions
If x=997,y=998andz=999, then the value of (x2+y2+z2−xy−yz−zx) is:
View SolutionIf x=6,y=4andz=3, then find the value of x2+y2+z2−2xy+2yz−2zx.
View SolutionIf x=997,y=998andz=999, then the value of (x2+y2+z2−xy−yz−zx) is:
View SolutionIf x+y+z=10,x3+y3+z3=75andxyz=15, then find the value of x2+y2+z2−xy−yz−zx
View SolutionIf x2+y2+z2=133,xy +yz + zx = 114 and xyz = 216, then the value of x3+y3+z3 is:
यदि x2+y2+z2=133 है, xy +yz + zx = 114 है तथा xyz = 216 है, तो x3+y3+z3 का मान क्या होगा ?View SolutionIf x=997 , y=998 z=999 then the value of x2+y2+z2−xy−yz−zx will be
View SolutionIf x=4,y=−2andz=3 then value of (cy+yz+zx)x+5y+3z is
View SolutionIf x+y+z=0 then what is the value of xy+yz+zxx2+y2+z2
View SolutionIf x + y + z = 22 and xy + yz + zx = 35 , then what is the value of (x−y)2+(y−z)2+(z−x)2 ?
View SolutionIf xy+yz+zx=1 then the value of 1+y2(x+y)(y+z) is
View Solution