In a cricket match highest score in a innings is 2 / 9 of the total score and second highest score is 2 / 9 of the rest score. If difference between highest and second highest scores is 8 runs. Then the total score is?
160
172
180
162
The correct Answer is:d
To solve the problem step by step, let's denote the total score of the cricket match as T.
Step 1: Define the highest score
According to the problem, the highest score is 29 of the total score. Therefore, we can express the highest score H as:
H=29T
Step 2: Calculate the remaining score after the highest score
The remaining score after accounting for the highest score is:
Remaining Score=T−H=T−29T=79T
Step 3: Define the second highest score
The second highest score is 29 of the remaining score. Thus, we can express the second highest score S as:
S=29(79T)=1481T
Step 4: Set up the equation based on the difference
We know that the difference between the highest score and the second highest score is 8 runs. Therefore, we can write the equation:
H−S=8
Substituting the expressions for H and S:
29T−1481T=8
Step 5: Find a common denominator and simplify
The common denominator for the fractions is 81. We can rewrite 29T as 1881T:
1881T−1481T=8
This simplifies to:
481T=8
Step 6: Solve for T
To find T, multiply both sides by 81:
4T=8×81
4T=648
Now divide both sides by 4:
T=6484=162
Conclusion
The total score T is:
162
According to the problem, the highest score is 29 of the total score. Therefore, we can express the highest score H as:
H=29T
The remaining score after accounting for the highest score is:
Remaining Score=T−H=T−29T=79T
The second highest score is 29 of the remaining score. Thus, we can express the second highest score S as:
S=29(79T)=1481T
We know that the difference between the highest score and the second highest score is 8 runs. Therefore, we can write the equation:
H−S=8
Substituting the expressions for H and S:
29T−1481T=8
The common denominator for the fractions is 81. We can rewrite 29T as 1881T:
1881T−1481T=8
This simplifies to:
481T=8
To find T, multiply both sides by 81:
4T=8×81
4T=648
Now divide both sides by 4:
T=6484=162
The total score T is:
162
Topper's Solved these Questions
Similar Questions
The highest score in an innings was 311 of the total score and the next highest was 311 of the remainder. If the socres differ by 18, find the total score.
View SolutionThe highest score in an inning was 31of the total and the next highest was 311of the remainder. If the scores differed by 9, the total score was.
View Solution
Knowledge Check
The highest score in an innings was 311 of the total score and the next highest was 311 of the remainder. If the socres differ by 18, find the total score.
A99B110C121D132The maximum score of runs in an innings was 3/11 of the total score. The second score in the same innings was the maximum score of 3/11 of the remaining runs. If the difference of both scores is 9, then what was the total score?
A106B146C118D121Who has scored the highest run in in a test cricket innings?
ASanath JayasuriyaBGarfield SobersCBrian LaraDHanif Mohammad
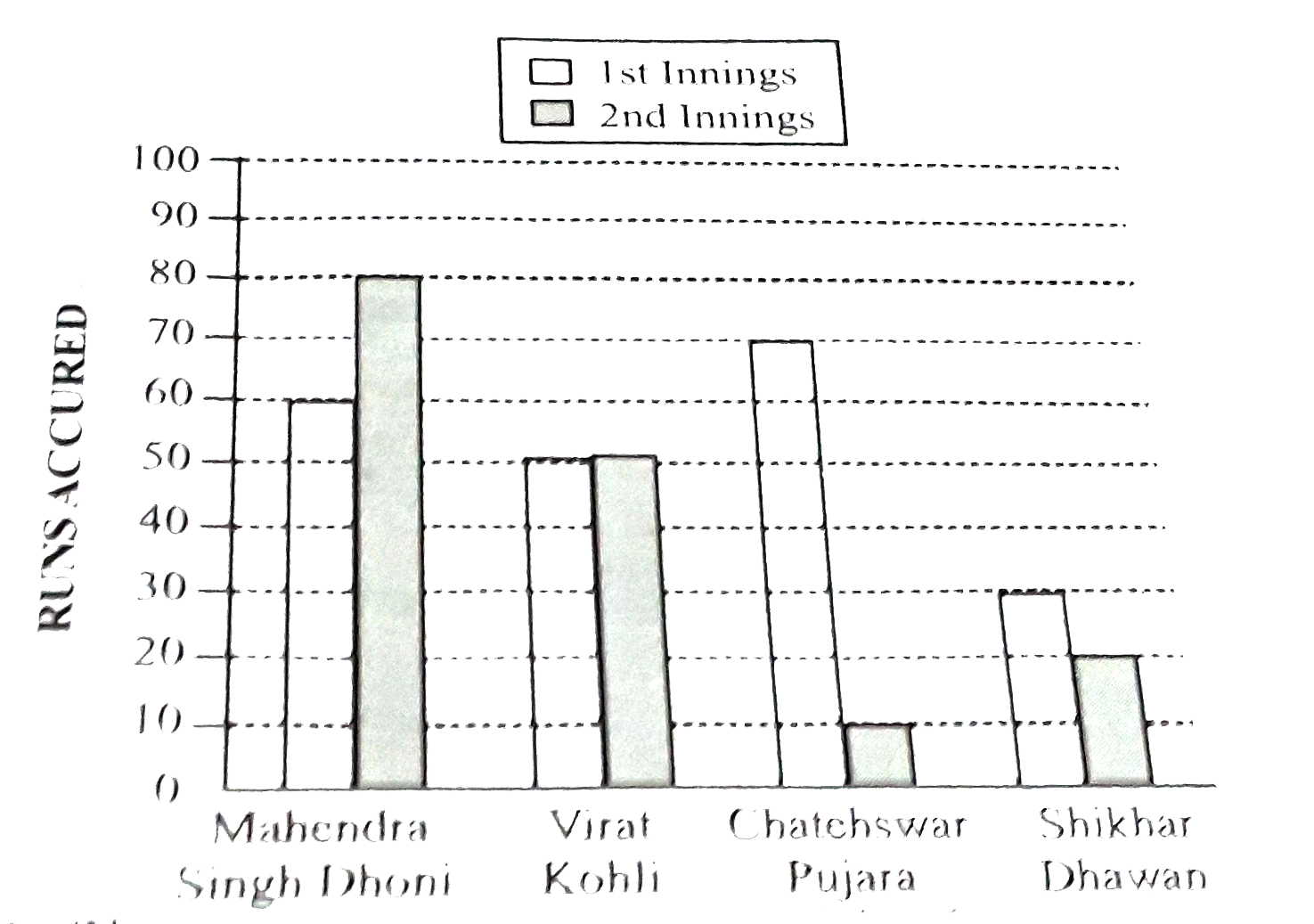
The averag run of two innins of the player scored highest in averages is :
View Solution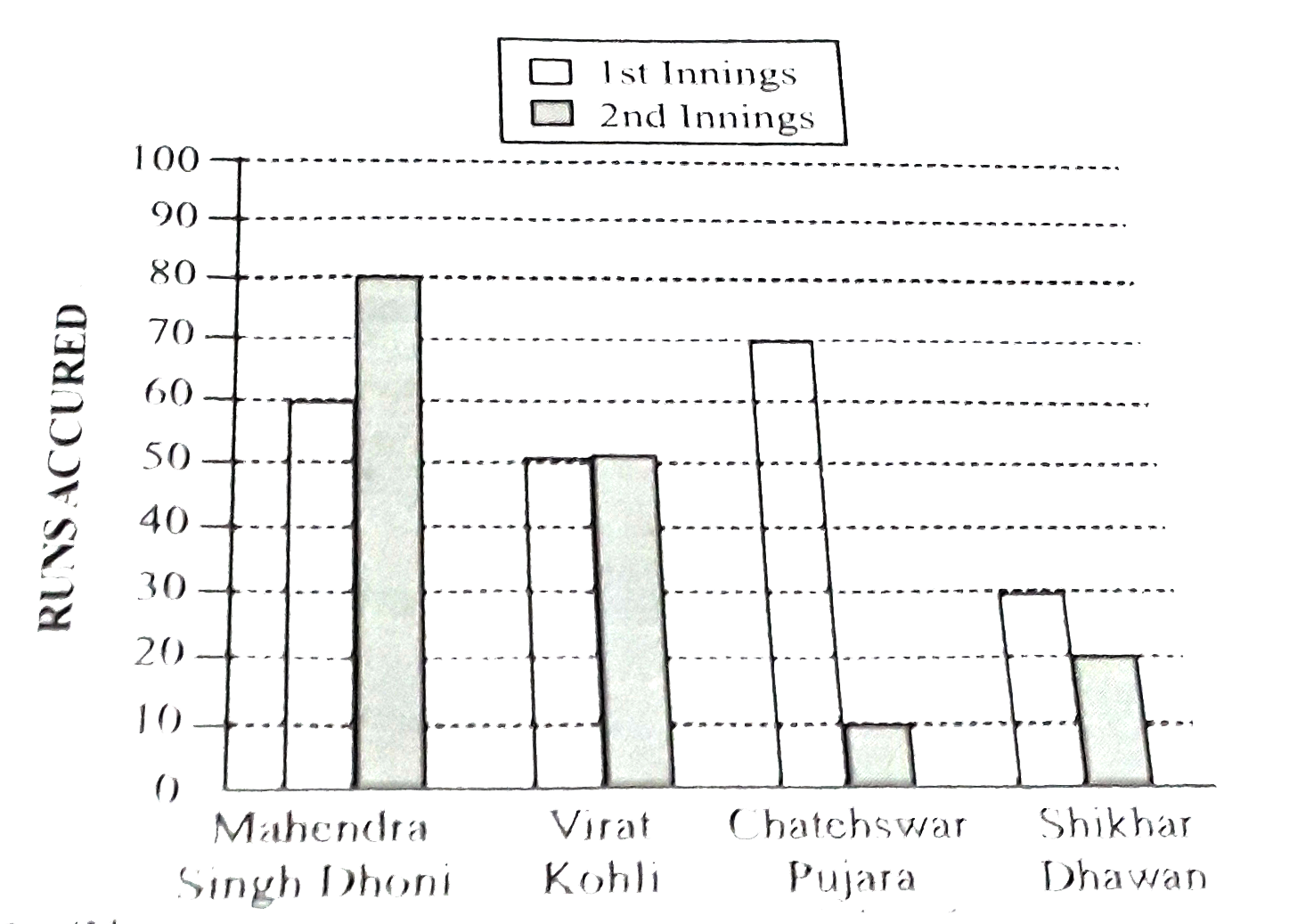
The total scores in the first innings contriburted by the players is :
View SolutionThe batting average for 40 innings of a cricket player is 50 runs. His highest score in an innings exceeds his lowest score by 172 runs. If these two innings are excluded, the average score of the remaining 38 innings is 48 runs. Find his highest score in an innings.
View SolutionIf the average of 64 innings of a batsman is 62. If highest and lowest innings are excluded then the average of remaining 62 innings is 60. If the difference between highest and lowest innings is 180 runs. Find his highest and lowest score.
View SolutionIf the average of 42 innings of a batsman is 30. If highest and lowest innings are excluded then the average of remaining 40 innings is 28. If the difference between highest and lowest innings is 100 runs. Find his highest and lowest score.
View Solution
