A block of mass m slides from rest at a height H on a frictionless inclined plane as shown in the figure. It travels a distance d across a rough horizontal surface with coefficient of kinetic friction μ , and compresses a spring of spring k by a distance x before coming to rest momentarily. Then the spring extends and the block travels back attaining a final height of h. Then
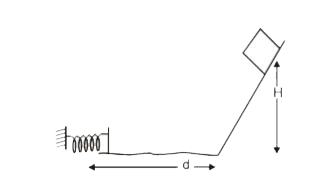
h=H−2μ(d+x)
h=H+2μ(d+x)
h=H−2μd+kx2/mg
h=H−2μ(d+x)+kx2/2mg
The correct Answer is:A
mgH−2μmg(d+x)−mgh=0
h=H−2μ(d+x)
Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-I ( PHYSICS)
20 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
19 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-I : PHYSICS
50 Videos
Similar Questions
A block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View SolutionA block of mass m moving at a speed v compresses as spring thrugh a distance x before its speed is halved. Find the spring constant of the spring.
View Solution
Knowledge Check
A block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :
 Amgh'=mgh−μmgdBmgh'=mgh+μmgdCmgh'=mgh+μmgd+kx2Dmgh'=mgh−μmgd−kx2
Amgh'=mgh−μmgdBmgh'=mgh+μmgdCmgh'=mgh+μmgd+kx2Dmgh'=mgh−μmgd−kx2A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
AmgBmg sin θCμmgcosθDμmgsinθA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
A block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
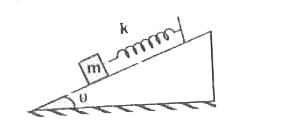
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
View SolutionA block of mass m is released on the top of a smooth inclined plane of length x and inclination θ as shown in figure. Horizontal surface is rough. If block comes to rest after moving a distabce d on the horizontal surface, then coefficient of friction between block and surface is :-

View SolutionA block of mass m is released from point (A) in figure. The track is frictionless except for the position between points (B) and (C), which has a length of dBC. The block travels down the track, hits a spring of force constant k, and compresses the spring x from its equilibrium position before coming at rest momentarily. Determine the coefficient of kinetic friction between the block and the rough surface between (B) and (C).

View Solution
