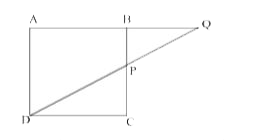
Let ABCD be a square and let P be point on segment CD such that DP : PC = 1 : 2. Let Q be a point on segment AP such that ∠BQP=90∘. Then the ratio of the area of quadrilateral PQBC to the area of the square ABCD is
3160
3760
3960
4160
The correct Answer is:D
Step by step video, text & image solution for Let ABCD be a square and let P be point on segment CD such that DP : PC = 1 : 2. Let Q be a point on segment AP such that angleBQP = 90^@. Then the ratio of the area of quadrilateral PQBC to the area of the square ABCD is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-I ( MATHEMATICS)
20 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( MATHEMATICS)
10 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II ( MATHEMATICS)
10 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
25 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-II(MATHEMATICS)
10 Videos
Similar Questions
If the length of the diagonal AC of a square ABCD is 5.2cm, then the area of the square is :
View SolutionIn the given figure, ABCD is a parallelogram. Point P is at BC such that PB : PC = 1 : 2. The extended DP and extended AB meets at point Q. If the area of BPQ is 20 unit2 then find the area of ΔDCP.
View Solution
Knowledge Check
Let ABCD be a square and let P be a point on AB such that AP:PB=1:2.if∠APD=θ, then what is the value of cosθ?
A1√10B1√5C2√10D2√5If the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
A15.12 sq. cmB13.52 sq. cmC12.62 sq. cmD10.00 sq. cm.If the length of the diagonal AC of a square ABCD is 5.2 cm, then the area of the square is :
A15.12 sq . CmB13.52 sq. cmC12.62 sq. cmD10 sq. cm
Let ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE= AF. Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
View SolutionABCD is a rectangle. P & Q are two points on AB, such that AP : PQ : QB = 3 : 4 : 5. Find the ratio of area ΔPQC and rectangle ABCD.
View SolutionABCD is a square and E is mid point of AD. If area of square is given by A1.

View SolutionIn a triangle ABC, let G denote its centroid and let M, N be points in the interiors of the segments AB, AC, respectively, such that M, G, N are collinear. If r denotes the ratio of the area of triangle AMN to the area of ABC then
View SolutionABCD is a parallelogram, P and Q are the points on the diagonal AC such that AP=QC, then quadrilateral BPDQ is a :
View Solution
