If in a triangle PQR;sinP,sinQ,sinR are in A.P; then (A)the altitudes are in AP (B)the altitudes are in HP (C)the altitudes are in GP (D)the medians are in APSolution in Punjabi
the altitudes are in AP
the altitudes are in HP
the medians are in GP
the medians are in AP
The correct Answer is:B
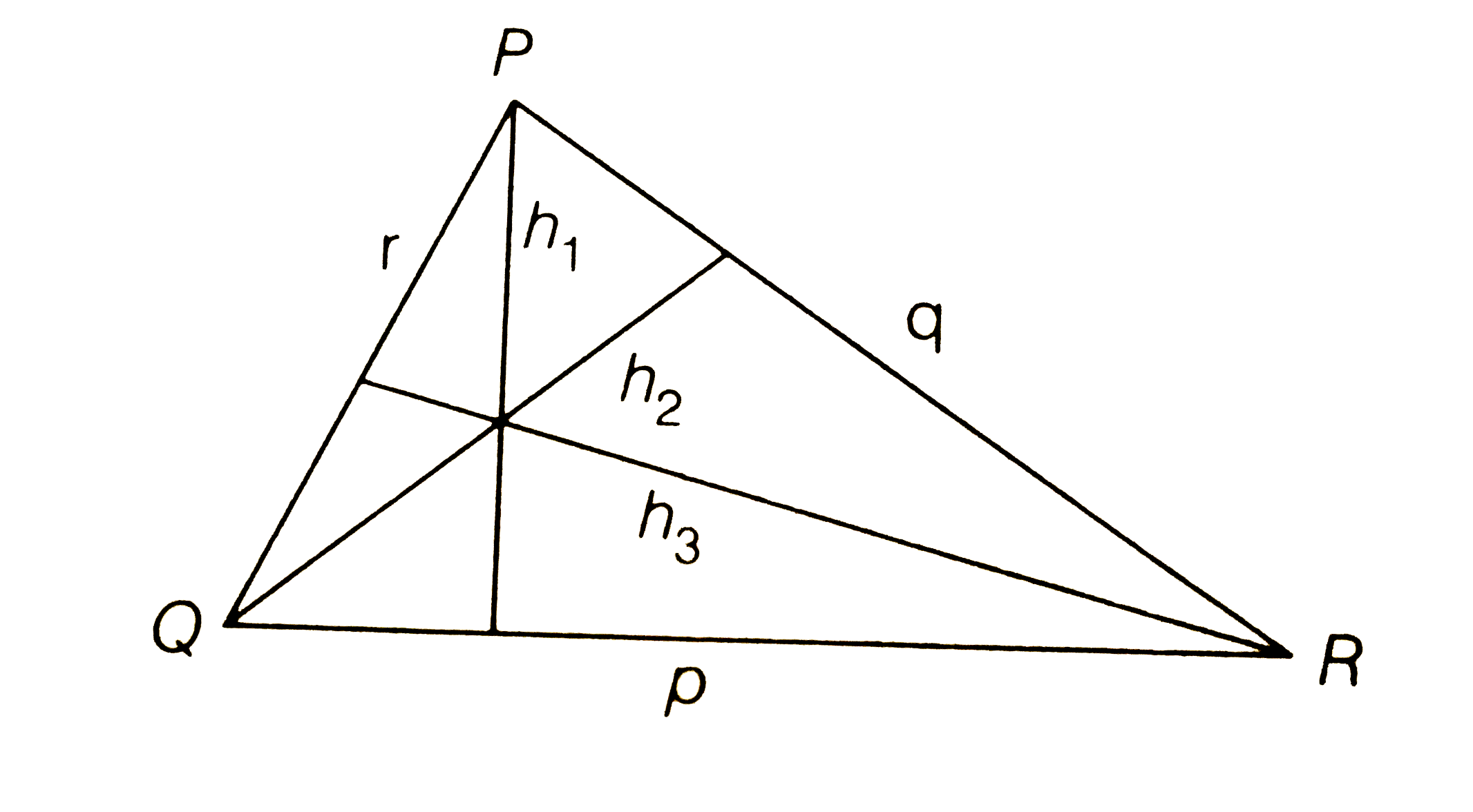
Let triangle be the area of ΔPQR.
∴Δ=12×p×h1 [h1,h2,h3 are altitudes ]
⇒h1=2Δp ….(i)
Similarly, h2=2Δq ….(ii)
and h3=2Δr ....(iii)
According to the question, sinP, sinQ, sin R are in AP.
Then, kp,kq,kr, are in AP [ by sine rule ]
⇒p,q,r are in AP.
⇒2Δh1,2Δh2,2Δh3 are in AP. [ by Eqs. (i),(ii) and (iii) ]
⇒1h1,1h2,1h3 are un AP.
⇒h1,h2,h3 are in HP.
⇒ Altitudes are in HP.
 .
.
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Passage Based Questions)
24 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 7
7 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
For a positive integer n let a(n)=1+12+13+14+.....+1(2n)−1. Then
View SolutionFind the value of x of equation 4x2=16
View SolutionThe minimum value of 4x+42−x,x∈R is
View SolutionProve that 2sin2(π6)−sec2(π3)=−72
View SolutionLet R={(3,3),(6,6),(9,9),(6,12),(3,9),(3,12),(12,12),(3,6)} is a relation on set A={3,6,9,12} then R is a) an equivalence relation b) reflexive and symmetric only c) reflexive and transitive only d) reflexive only
View SolutionIf sin(B+C−A),sin(C+A−B),sin(A+B−C), are A.P.,thencotA,cotB,cotCare∈ GP (b) HP (c) AP (d) none of these
View SolutionIf P is a point on the altitude AD of the triangle ABC such the ∠CBP=B3, then AP is equal to 2asinC3 (b) 2bsinC3 2csinB3 (d) 2csinC3
View SolutionIf in a Delta ABC, the altitudes from the vertices A,B,C on opposite sides are in H.P.then sin Asin B, sin C are in
View SolutionLet the positive numbers a,b,c,d be in AP. Then abc,abd,acd,bcd are (2001, 1M) not in AP/GP/HP (b) in AP in GP (d) in HP
View SolutionIf in a triangle PQR;sinP,sinQ,sinR are in A.P; then
View SolutionIf, in a △PQR, sin P, sin Q, sin R are in the A.P, then its altitudes are in
View SolutionIf in a ΔPQR, sin P, sin Q , sin R are in AP, then:
View SolutionIf in a triangle ABC, the altitudes from the A,B,C on opposite sides are in H.P. then sinA, sin B, sin C are in
View SolutionIf a, b, c are in A.P., p, q, r are in HP and ap, bq, cr are in GP, then Pr+rP is equal to
View SolutionIF in a ΔABC , the altitudes from the vertices A,B,C on opposite sides are in H.P , then sin A , sin B , sin C are in
View SolutionIf in a triangle PQR,sinP,sinQ,sinRareinA.P. , then (a)the altitudes are in A.P. (b)the altitudes are in H.P. (c)the medians are in G.P. (d)the medians are in A.P.
View Solution
