If 2λ,λ and [λ2−14],λ∈R−{0} and [⋅] denotes the gratest integer function are the first three terms of a GP in order, then the 51th term of the sequence, 1,3λ,6λ,10λ,…., is Solution in Punjabi
5104
5304
5504
5704
The correct Answer is:B
∴2λ,λ,[λ2−14] are oin GP, then
λ2=2λ[λ2−14]
⇒λ2=[λ2−14]
∴λ must be an evenm integer
Hence, λ=4
Now, reqyured sequence 1,12,24,40,…..
or 1,4(1+2),4(1+2+3),4(1+2+3+4),....
∴51th term =4(1+2+3+....+51)
=4⋅512(1+51)=4⋅51⋅26=5304
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 1
5 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 2
11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
First term of a sequence is 1 and the (n+1)th term is obtained by adding (n+1) to the nth term for all natural numbers n, the 6th term of the sequence is
View SolutionIf nth term of the series 25+29+33+37...... and 3+4+6+9+13+........ are equal, then n equal
View SolutionProve that 2sin2(π6)−sec2(π3)=−72
View SolutionLet R={(3,3),(6,6),(9,9),(6,12),(3,9),(3,12),(12,12),(3,6)} is a relation on set A={3,6,9,12} then R is a) an equivalence relation b) reflexive and symmetric only c) reflexive and transitive only d) reflexive only
View SolutionIf |x||,|x-1|,|x+1| are first three terms of an A.P.then sum of the first to terms is lambda, the value of (lambda)/(5) is equal to
View SolutionPortion of asymptote of hyperbola x^2/a^2-y^2/b^2 = 1 (between centre and the tangent at vertex) in the first quadrant is cut by the line y + lambda(x-a)=0 (lambda is a parameter) then (A) lambda in R (B) lambda in (0,oo) (C) lambda in (-oo,0) (D) lambda in R-{0}
View Solutionp(lambda)^4+q(lambda)^3+r(lambda)^2+s(lambda)+t = |((lambda^2 + 3lambda) , lambda -1 , lambda+3) , (lambda +1 , -2lambda , lambda-4 ) ,(lambda-3 , lambda+4 , 3lambda)| find t=?
View SolutionA=[[1,4, of matrix 1,8,8 lambda-6lambda,8,8 lambda-61+lambda^(2),8 lambda+4,2 lambda+21]]
View SolutionThe vertices of a triangle ABC are (lambda,2-2lambda), (-lambda + 1, 2lambda) and (-4-lambda, 6-2lambda). If its area be 70 units then number of integral values of lambda is (a) 1 (b) 2 (c) 4 (d) 0
View SolutionThe equation x^(3)-6x^(2)+9x+lambda=0 have exactly one root in (1,3) then [lambda+1] is (where [.] denotes the greatest integer function)
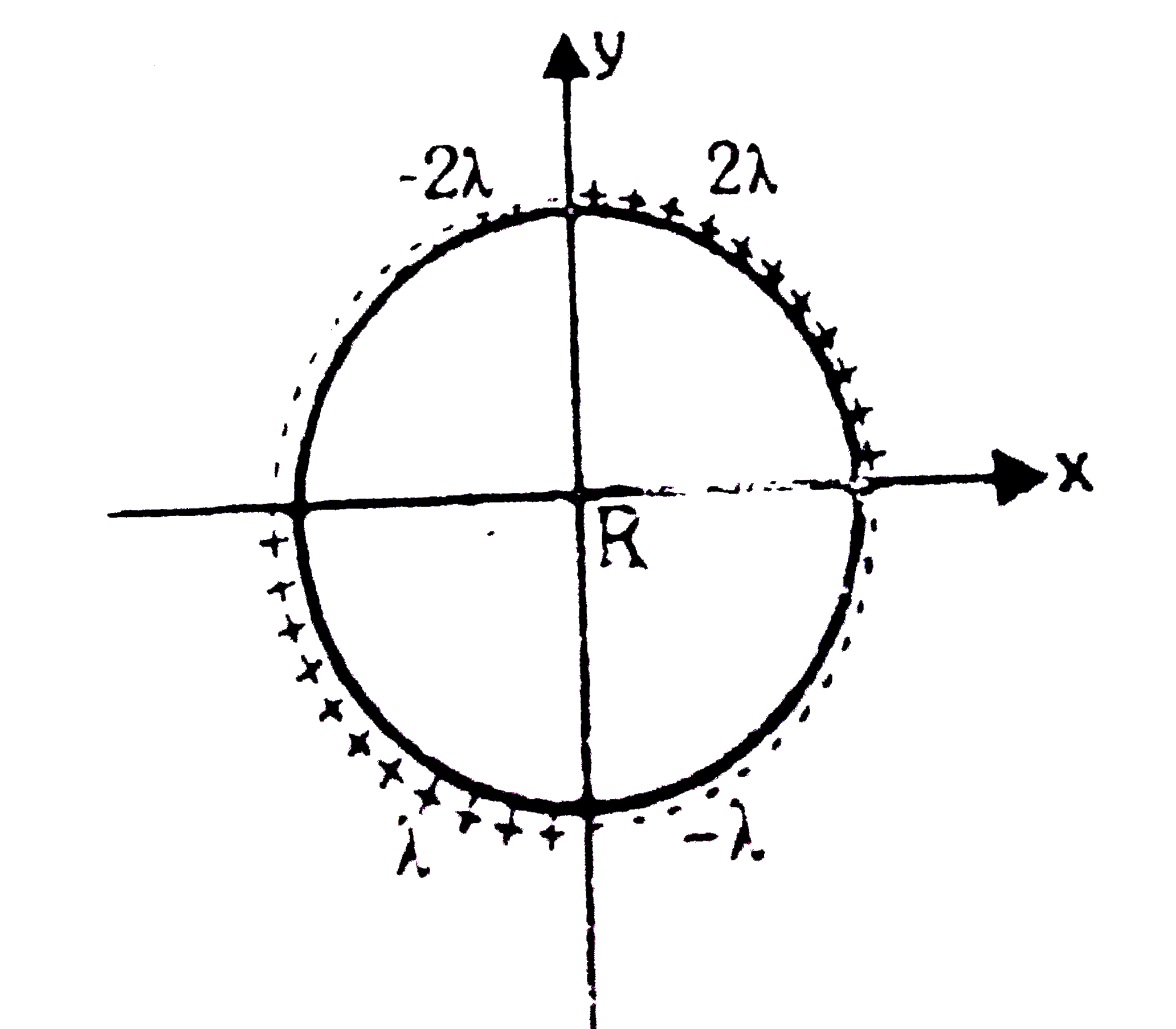
View SolutionThe charge per unit length of the four quadrant of the ring is 2λ,−2λ,λ and −λ respectively. The electric field at the centre is:
View SolutionLet pλ4+qλ3+rλ2+sλ+t=∣∣ ∣ ∣∣λ2+3λλ−1λ−3λ−1−2λλ−4λ−3λ+3 3λ∣∣ ∣ ∣∣be an identity in λ where p,q,r,s and t are constants. Then the value of t is
View SolutionIf λ→i+2λ→j+2λ→k is a unit vector then the value of λ is ……………
View Solutionif points (2lambda, 2lambda+2) , (3, 2lambda + 1) And (1,lambda + 1) are linear, then lambda find the value of
View SolutionPortion of asymptote of hyperbola x2a2−y2b2=1 (between centre and the tangent at vertex) in the first quadrant is cut by the line y+λ(x−a)=0 (lambda is a parameter) then (A) λ∈R (B) λ∈(0,∞) (C) λ∈(−∞,0) (D) λ∈R−{0}
View Solutionसमतल r=(1+λ−μ)i+(2−λ)j+(3−2λ+2μ)k का कार्तीय समीकरण है
View Solution
