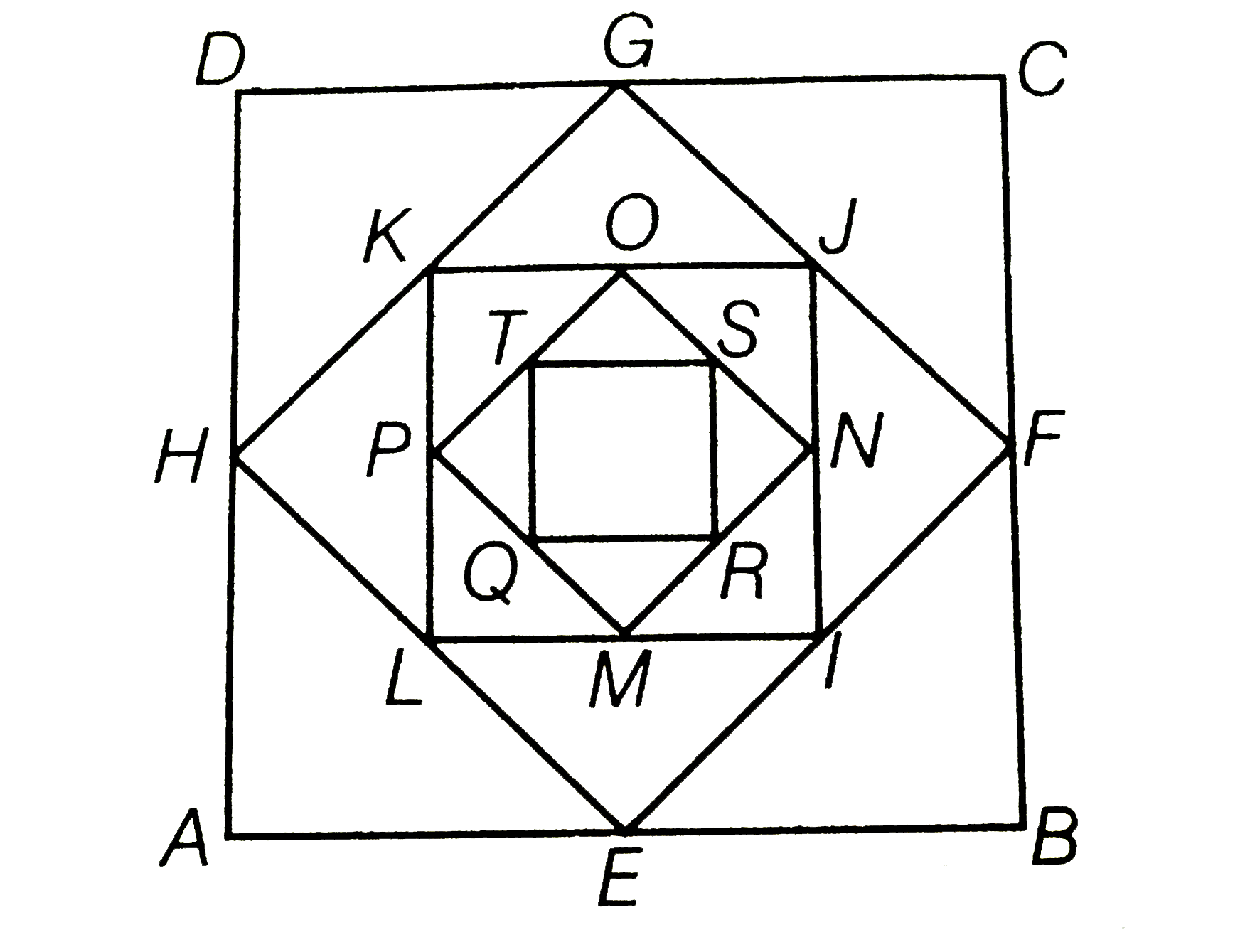
A square is drawn by joining mid pint of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued in definitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?Solution in Punjabi
Let a be the side lengh of square, than
AB=BC=CD=DA=a
∴ E,F,G,H are the mid-points of AB,BC,CD and DA, respectively.
∴EF=FG=GH=HE=a√2
and I,J,K,L are the mid-points of EF,FG,GH and HE, respectively.
∴IJ=JK=KL=LI=a2
Similarly, MN=NO=OP=PM=a2√2 and QR=RS=ST=TQ=a4,.....
S=Sum of areas =ABCD+EFGH+IJKL+MNOP+QRST+...
a2+(a√2)2+(a√2)2+(a2√2)2+....
=a2(1+12+14+18+...)
=a2⎛⎝11−12⎞⎠=2a2=2(16)2 [∴a=16 cm ]
=512sq cm
 .
.
Topper's Solved these Questions
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise For Session 1
Explore 5 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHSChapter:SEQUENCES AND SERIESExercise:Exercise For Session 2
Explore 11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHSChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 12 Videos
Similar Questions
First term of a sequence is 1 and the (n+1)th term is obtained by adding (n+1) to the nth term for all natural numbers n, the 6th term of the sequence is
View SolutionIf nth term of the series 25+29+33+37...... and 3+4+6+9+13+........ are equal, then n equal
View SolutionProve that 2sin2(π6)−sec2(π3)=−72
View SolutionLet R={(3,3),(6,6),(9,9),(6,12),(3,9),(3,12),(12,12),(3,6)} is a relation on set A={3,6,9,12} then R is a) an equivalence relation b) reflexive and symmetric only c) reflexive and transitive only d) reflexive only
View SolutionA square is drawn by joining the mid-points of the sides of a square. A third square is drawn inside the second square in the same way and the processes continued indefinitely. If the side of the square is 10cm , find the sum of the areas of all the squares so formed.
View SolutionProve that the sum of the areas of the squares drawn on the sides of a rhombus is equal to the sum of the areas of two squares drawn on the diagonals of the given square.
View Solutionएक वर्ग की एक भुजा 10 सेमी है । भुजाओं के मध्य बिंदुओं को मिलाकर एक दूसरा वर्ग बनाया गया है जिसके मध्य बिन्दुओं को मिलाकर पुनः एक अन्य वर्ग बनाया गया है । यह प्रक्रिया अनन्त बार दुहराई गई है । सभी वर्गों का क्षेत्रफल ज्ञात कीजिए ।
View SolutionA square is drawn by joining the mid points of the sides of a square. A third square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 15 cm, then find the sum of the areas of all the squares so formed.
View SolutionIn the figure shown square II is formed by joining the mid-points of square I
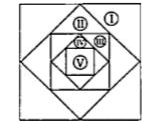
and so on . In this way total five squares are drawn . The sides of the square I is 'a' cm.
What is the perimeter of all the five squres ?
View SolutionIn the figure shown square II is formed by joining the mid-points of square II
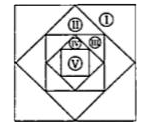
and so on . In this way total five squares are drawn . The sides of the square I is 'a' cm.
What is the total area of all the five squares ?
View SolutionA square is drawn by joining the mid points of the sides of a given square. A third square is drawn inside the second square in the same way and this process continues indefinitely. If a side of the first square is 4 cm, determine the sum of the areas of all the squares :
View SolutionA square is drawn by joining the mid-points of the sides of a square. A third square is drawn inside the second square in the same way and the processes continued indefinitely. If the side of the square is 10cm , find the sum of the areas of all the squares so formed.
View Solutiona भुजा वाले समबाहु त्रिभुज के अन्तःवृत्त के अन्दर वर्ग खींचा गया है, तो वर्ग का क्षेत्रफल है।
View Solutiona भुजा वाले समबाहु त्रिभुज के अन्तःवृत्त के अन्दर वर्ग खींचा गया है, तो वर्ग का क्षेत्रफल है।
View SolutionThe side of a given square is 10cm. The mid points of its sides are joined to form a new square. Again the mid poind of the sides of this new square are joined to form another square. This process is continued indefinitely. Find the sum of the area.
View SolutionA square is drawn by joining the mid points of the sides of a square. A third square is drawn inside the second square in the same way and the process is continued infinitely. If the side of the square is 10 cms, find the sum of the areas of all the squares so formed.
View Solution

