If →a,→b are any two vectors, then give the geometrical interpretation of relation ∣∣→a+→b∣∣=∣∣→a−→b∣∣Solution in Punjabi
Let OA=a and AB=b. completing the parallelogram OABC.
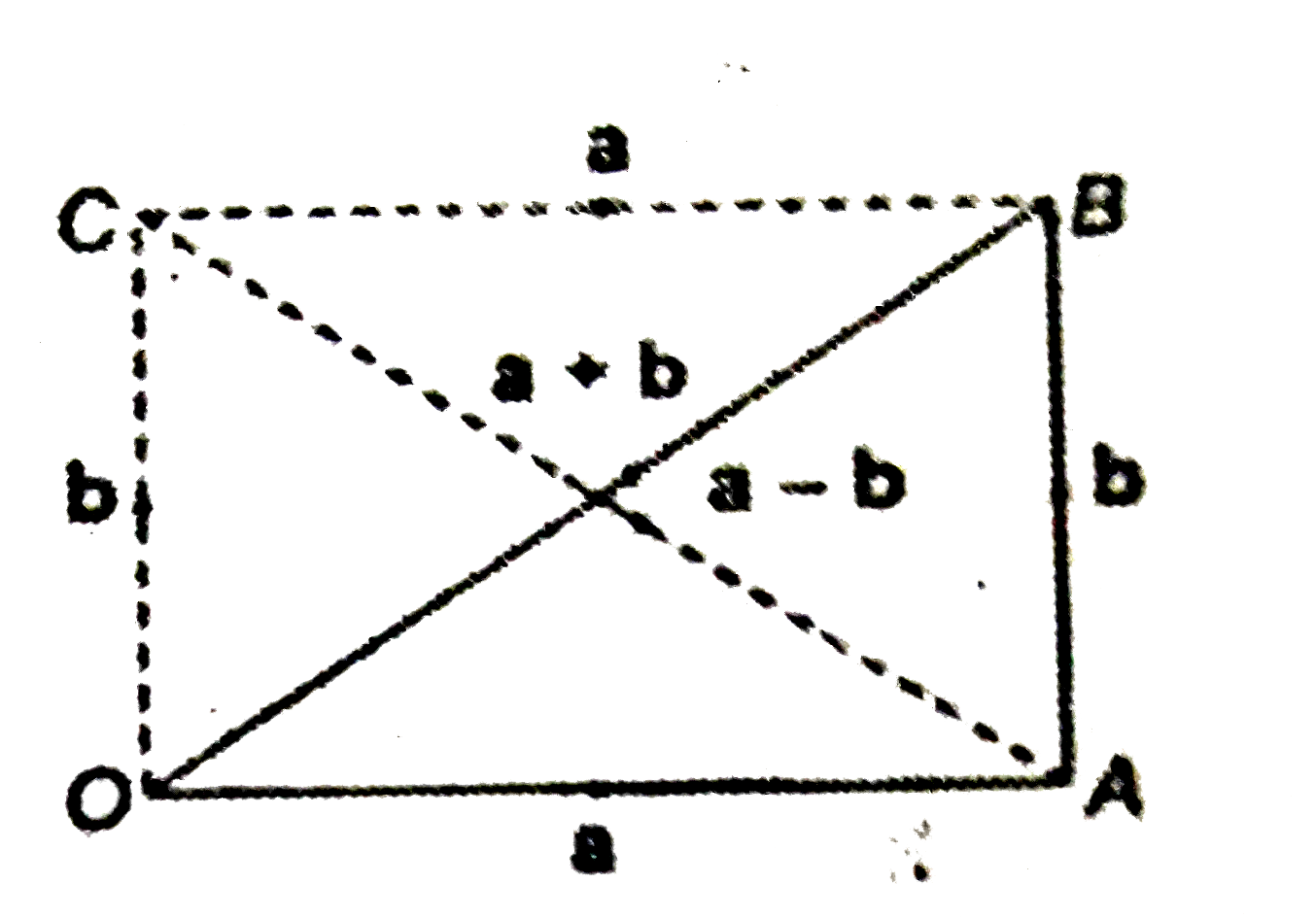
Then, OC=b and CB=a
from ΔOAB, we have
OA+AB=Ob⇒a+b=OB . . . (i)
From ΔOCA, we have
OC+CA=OA
⇒b+CA=a⇒CA=a−b . . . (ii)
Clearly, |a+b|=|a−b|⇒|OB|=|CA|
Diagonals of parallelogram OABC are qual.
OABC is a rectangle.
⇒OA⊥OC⇒a⊥b.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
Classify the following measure as scalar and vector: 10Kg
View SolutionIf a=2ˆi−ˆj+2ˆkandb=−ˆi+ˆj−ˆk, then find a+b. Also, find a unit vector along a+b.
View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
View SolutionFor any two vectors →a and →b, we always have ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
View Solutionfor any two vectors vec a and vec b, show that |vec a*vec b|<=|vec a||vec b|
View SolutionFor any two vectors vec a, vec b | vec a * vec b | <= | vec a || vec b |
View SolutionIf →a and →b are two vectors such that (→a+→b).→a−→b=0 find the relation between the magnitudes of →a and →b.
View SolutionFor any two vectors →a and →b write when ∣∣→a+→b∣∣=|→a|+∣∣→b∣∣ holds.
View SolutionFor any two vectors →a and →b write when ∣∣→a+→b∣∣=∣∣→a−→b∣∣ holds.
View SolutionProve that (→a−→b)×(→a+→b)=2(→a×→b) and interpret it geometrically.
View SolutionFor any two vectors vec a and vec b prove that | vec a + vec b | <= | vec a | + | vec b |
View SolutionDefine the vector product of two vectors →aand→b . Give geometrical interpretation of →a×→b . Show that the satisfies the distributive law .
View SolutionFor any two vectors →aand→b , show that ∣∣→a.→b∣∣≤|→a|∣∣→b∣∣
View Solution(a) What is the geometric significance of the relation ∣∣→a+→b∣∣=∣∣→a−→b∣∣ ?
(b) Prove geometrically that ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣.
View SolutionShow that |→a|→b−∣∣→b∣∣→a, for any two non - zero vectors →a and →b.
View SolutionProve that (→a−→b)×(→a+→b)=2(→a×→b) and interpret it geometrically.
View Solution

