If ABCDEF is a regular hexagon and AB+AC+AD+AE+AF=λAD, then λ is equal toSolution in Punjabi
We have,
AD+EB+FC=(AB+BC+CD)+(ED+DC+CB)+FC
=AB+(BC+CB)+(CD+DC)+ED+FC
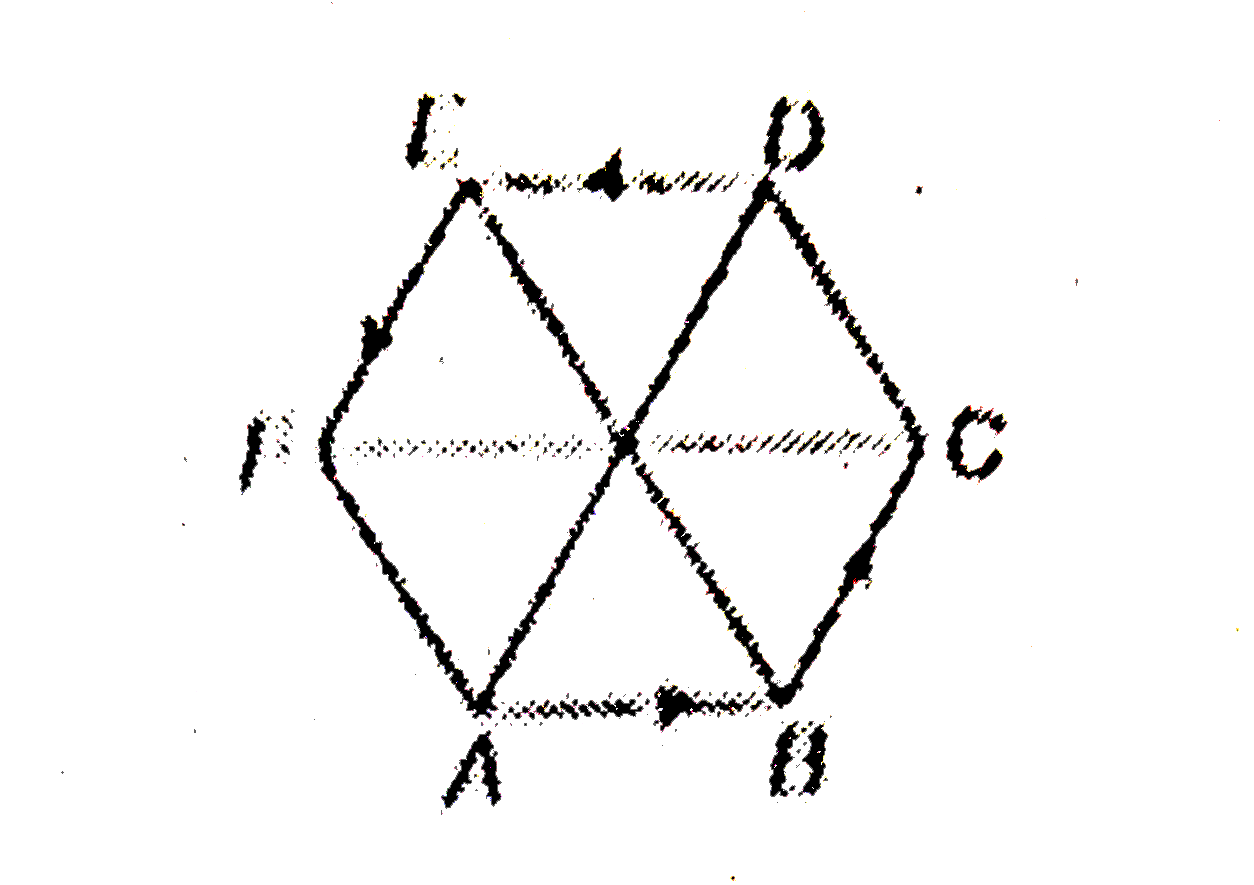
=AB+O+O+AB+2AB=4AB
(∵ED=AB,FC=2AB) hence proved.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
Classify the following measure as scalar and vector: 10Kg
View SolutionIf a=2ˆi−ˆj+2ˆkandb=−ˆi+ˆj−ˆk, then find a+b. Also, find a unit vector along a+b.
View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
View SolutionIf ABCDEF is a regular hexagon inscribed in a ( circle with centre O, then the value of )/(AB)+bar(AC)+bar(AD)+( then the value of )/(AF) equals
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View SolutionIf ABCDEF is a regular hexagon with centre O , then P.T ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=3¯¯¯¯¯¯AD=6¯¯¯¯¯¯AO
View SolutionIf ABCDEF is a regular hexagon and AB+AC+AD+AE+AF=λAD then λ is equal to
View SolutionIf ABCDEF is a regular hexagon with centre O , then P.T ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=3¯¯¯¯¯¯AD=6¯¯¯¯¯¯AO
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionABCDEF is a regular hexagone. AB+AC+AD+AE+AF=λAD then λ = ………….
View SolutionIn a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View SolutionConsider the regular hexagon ABCDEF with centre at O (origin). Five forces vec(AB), vec(AC), vec(AD), vec(AE), vec(AF) act at the vertex A of a regular hexagon ABCDEF. Then their resultant is
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionIn a regular hexagon ABCDEF,−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=k−−→AD then k is equal to
View Solution
