Question

Find n, if $(n+2)!=60\times (n-1)!$

Explanation

First we show that the product of p consecutive positive integers is divisible by p!. Let the p consecutive integers be m,m+1,m+2, . . ,m+p-1. then,
`m(m+1)(m+2) . . (m+p-1)=((m+p-1)!)/((m-1))`
`=p!((m+p-1)!)/((m-1)!p!)`
`=p!.^(m+p-1)C_(p)`
Since, `.^(m+p-1)C_(p)` is an integer
`therefore.^(m+p-1)C_(p)=(m(m+1)(m+2). . .(m+p-1))/(p!)`
Now, `(n!)!` is the product of the positive integers from 1 to n!. we write the integers from 1 to n! is (n-1)! rows as follows:
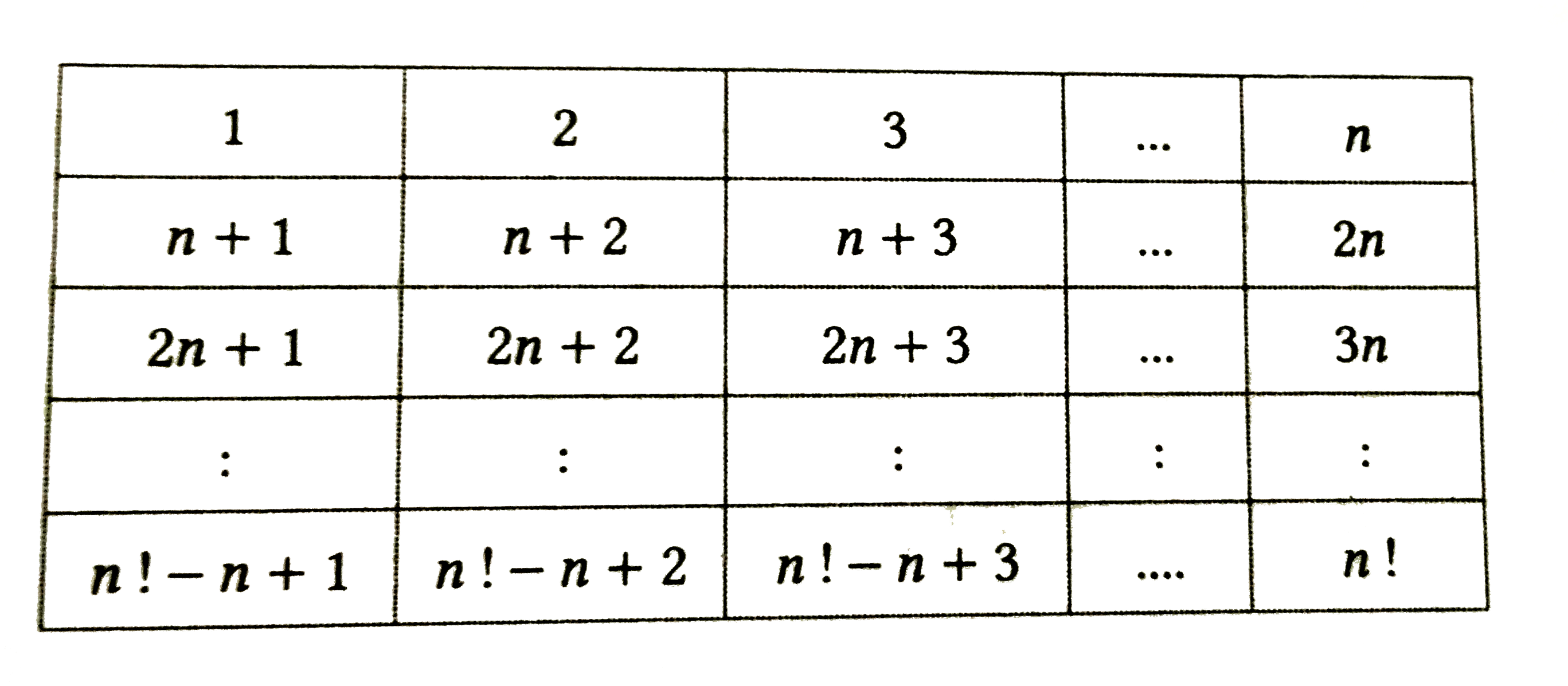ltBrgt Each of these (n-1)! rows contains n consecutive positive integers. the products of the conescutive integers in each row is divisible by n!. thus, the product of all the integers from 1 to n! is divisible by `(n1)^((n-1)!)`.