If α,β are the roots of the equation x2−2x−a2+1=0 and γ,δ are the roots of the equation
x2−2(a+1)x+a(a−1)=0 such that α,βεn(γ,δ) find the value of a.Solution in Punjabi
The correct Answer is:aε(−14,1)
Since the given equation is
x2−2x−a2+1=0
⇒(x−1)2=a2
∴x−1≠a or x=1±a
∴α=1+a and β=1−a
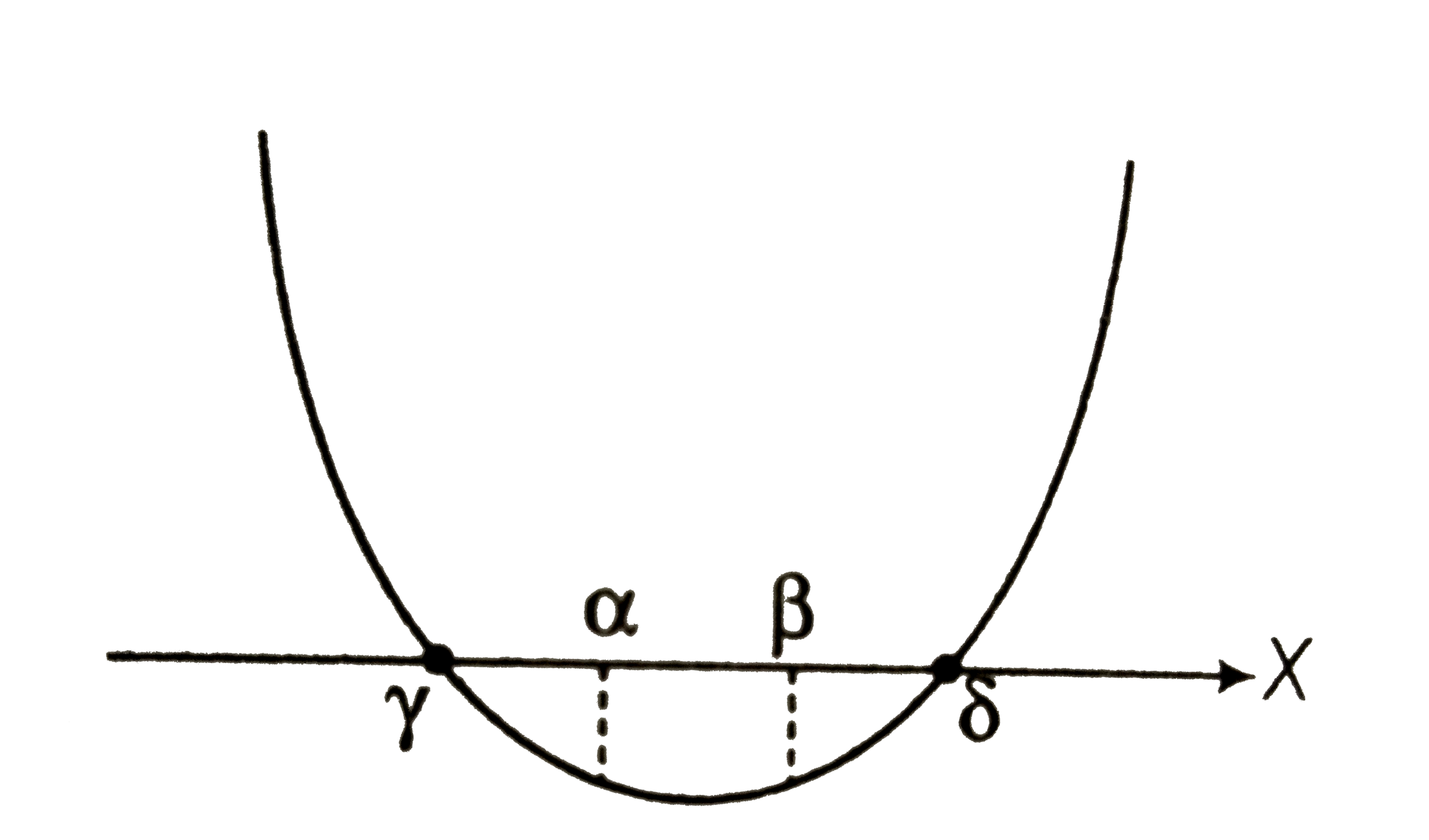
Let f(x)=x2−2(a+1)x+a(a−1) thus the following conditiions hold good:
Consider the followign cases:
Case I D>0
⇒4(a+1)2−4a(a−1)>0
⇒3a+1>0
∴a>−13
Case IIf(α)<0
⇒f(1+a)<0
⇒(1+a)2−2(1+a(1+a)+a(a−1)<0
⇒−(1+a)2+a(a−1)<0
⇒−3a−1<0
⇒a>−13
Case II f(s)=0
⇒f(1−a)<0
⇒(1−a)2−2(a+1)(1−a)+a(a−1)<0
⇒(4a+1)(a−1)<0
∴−14<a<1
Combining all cases we get
aε(−14,1)
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 35 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHSChapter:THEORY OF EQUATIONSExercise:Exercise (Statement I And Ii Type Questions)
Explore 7 Videos
- THE STRAIGHT LINESBook:ARIHANT MATHSChapter:THE STRAIGHT LINESExercise:The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
Explore 1 Video
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHSChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
Explore 2 Videos
Similar Questions
In the quadratic equation ax2+bx+c=0. if δ=b2−4ac and α+β,α2+β2,α3+β3 are in G.P. and α,β are the roots of ax2+bx+c=0
View SolutionStatement -1 If the equation (4p−3)x2+(4q−3)x+r=0 is satisfied by x=a,x=b nad x=c (where a,b,c are distinct) then p=q=34 and r=0
Statement -2 If the quadratic equation ax2+bx+c=0 has three distinct roots, then a, b and c are must be zero.
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionIf alpha,beta,gamma,delta are the roots of the equation x^(4)+x^(2)+1=0 then the equation whose roots are alpha^(2),beta^(2),gamma^(2),delta^(2) is
View SolutionIf alpha,beta are the roots of the equation x^(2)+px+1=0 gamma,delta the roots of the equation x^(2)+qx+1=0 then (alpha-gamma)(alpha+delta)(beta-gamma)(beta+delta)=
View SolutionLet alpha,beta be the roots of the equation x^(2)+ax+b=0 and gamma,delta be the roots of x^(2)-ax+b-2 If alpha beta gamma delta=24 and / alpha+(1)/(beta)+(1)/(gamma)+(1)/(delta)=(5)/(6), then find the value of a.
View SolutionLet alpha,beta be the roots of the equation x^(2)+ax+b=0 and gamma,delta be the roots of x^(2)-ax+b-2=0 lf alpha beta gamma delta=24 and (1)/(alpha)+(1)/(beta)+(1)/(gamma)+(1)/(delta)=(5)/(6), then find the value of a.
View Solutionif alpha,beta the roots x^(2)+x+2=0 and gamma,delta the roots of x^(2)+3x+4=0 then find the value of (alpha+gamma)(alpha+delta)(beta+gamma)(beta+delta)
View SolutionIf alpha,beta,gamma and delta are roots of equation x^(4)-7x^(2)+x-5=0, then the value of (alpha+beta+gamma)(alpha+beta+delta)(beta+gamma+delta)(alpha+gamma+delta) is equal to
View SolutionIf alpha,beta,gamma are the roots of the equations x^(4)-2x^(3)+2x^(2)+1=0 then the equation whose roots are 2+(1)/(alpha),2+(1)/(beta),2+(1)/(gamma),2+(1)/(delta) is
View SolutionLet alpha,beta be the roots of the equation x^(2)-(2a+1)x+a=0 and gamma,delta be the roots of the equation x^(2)+(a-4)x+a-1=0. If (alpha)/(gamma)-(delta)/(beta)=(alpha delta(alpha-gamma+beta-delta))/(a) then the value of (a-1)^(-2) is
View Solutionयदि α और β समीकरण x2+px−q=0 के तथा γ,δ समीकरण x2+px+r=0 के मूल हैं, तो सिद्ध कीजिए की, (α−γ)(α−δ)=(β−γ)(β−δ)=q+r
View SolutionIf α,β,γandδ are the roots of the equation x4−bx−3=0, then an equation whose roots are α+β+γδ2,α+β+δγ2,α+δ+γβ2,andδ+β+γα2, is:
View SolutionIf α,β are the roots of x2+px+1=0 and γ,δ are the roots of x2+qx+1=0 then (α−γ)(β−γ)(α+δ)(β+δ)=
View SolutionIf αandβ are the roots of the equation x2+px+1=0,gamam,δ are the roots of (x2+qx+1=0 , then , find (α−γ)(β−γ)(α+δ)(β+δ)
View Solution

