The solution of 33x−5=19x is
52
5
1
73
The correct Answer is:C
To solve the equation 33x−5=19x, we can follow these steps:
Step 1: Rewrite 9x in terms of base 3
We know that 9=32. Therefore, we can rewrite 9x as:
9x=(32)x=32x
So, we have:
19x=132x=3−2x
Step 2: Rewrite the equation
Now, we can rewrite the original equation:
33x−5=3−2x
Step 3: Set the exponents equal to each other
Since the bases are the same (both are base 3), we can set the exponents equal to each other:
3x−5=−2x
Step 4: Solve for x
Now, we can solve for x by isolating it:
1. Add 2x to both sides:
3x+2x−5=0⟹5x−5=0
2. Add 5 to both sides:
5x=5
3. Divide by 5:
x=1
Conclusion
The solution to the equation 33x−5=19x is:
1
---
We know that 9=32. Therefore, we can rewrite 9x as:
9x=(32)x=32x
So, we have:
19x=132x=3−2x
Now, we can rewrite the original equation:
33x−5=3−2x
Since the bases are the same (both are base 3), we can set the exponents equal to each other:
3x−5=−2x
Now, we can solve for x by isolating it:
1. Add 2x to both sides:
3x+2x−5=0⟹5x−5=0
2. Add 5 to both sides:
5x=5
3. Divide by 5:
x=1
The solution to the equation 33x−5=19x is:
1
Topper's Solved these Questions
- EXPONENTS AND POWERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - EXPONENTS AND POWERSEXERCISE - Exercise (Multiple Choice Questions) LEVEL - 2
15 Videos
- EXPONENTS AND POWERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - EXPONENTS AND POWERSEXERCISE - Exercise (Match the Following)
3 Videos
- EXPONENTS AND POWERSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - EXPONENTS AND POWERSEXERCISE - NCERT Section (Exercise 12.2)
17 Videos
- DIRECT AND INVERSE PROPORTIONSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DIRECT AND INVERSE PROPORTIONSEXERCISE - OLYMPIAD/HOTS CORNER
15 Videos
- FACTORISATIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FACTORISATIONEXERCISE - OLYMPIAD/HOTS CORNER
10 Videos
Similar Questions
Knowledge Check
The solution of inequality 37−(3x+5)≥9x−8(x−3) on number line is
A B
B C
C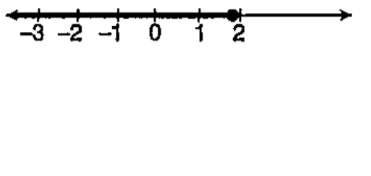 DNone of the above
DNone of the aboveThe solution set of 2x−13≥(3x−24)-((2-x)/5) is….A… Here, A refers to
A(−∞,2)B(−∞,2]C(−00,−12)D(−∞,−12]The solution set of (35)x=x−x2−9 is
A{0}B{1}CϕDnone of these
Find the general solution of sin5xcos3x=sin9xcos7x
View SolutionThe solution of the equation 34(x−1)=x−3 is:
(a) x=8
(b) x=9
(c) x=7
(d) x=6
View SolutionThe solution of the equation 9x−2x+12=2x+32−32x−1
View SolutionFor which equation(s) is x= 3 a solution?
(I) 2x−5+3x=10 (II) −x+72=2
(III) 4x−11=17 (IV) 9=−(x−1)+11
View SolutionThe value of 9x(9x−1)x9x+1.32x−2{729x381}−x÷3a−23.3a−23a−3a−1 is
View Solution
