A ceiling fan having 4 blades has a rotational symmetry of the order Find K.
The correct Answer is:2
To find the value of K in the rotational symmetry of the ceiling fan with 4 blades, we can follow these steps:
Step 1: Understand the concept of rotational symmetry
Rotational symmetry refers to the number of times a shape can be rotated around a central point and still look the same within one complete turn (360 degrees).
Step 2: Identify the number of blades
The ceiling fan has 4 blades. We can label them as A, B, C, and D.
Step 3: Determine the angles of rotation
Since there are 4 blades, we can find the angle of rotation for each symmetry position. The angle of rotation can be calculated as:
Angle of rotation=360∘Number of blades=360∘4=90∘
Step 4: Identify the positions after rotation
- When the fan is rotated by 90∘:
- Blade A moves to the position of Blade B
- Blade B moves to the position of Blade C
- Blade C moves to the position of Blade D
- Blade D moves to the position of Blade A
- When the fan is rotated by 180∘:
- Blade A moves to the position of Blade C
- Blade B moves to the position of Blade D
- Blade C moves to the position of Blade A
- Blade D moves to the position of Blade B
- When the fan is rotated by 270∘:
- Blade A moves to the position of Blade D
- Blade B moves to the position of Blade A
- Blade C moves to the position of Blade B
- Blade D moves to the position of Blade C
- When the fan is rotated by 360∘:
- All blades return to their original positions.
Step 5: Count the number of symmetries
From the above rotations, we can see that the fan looks the same after:
1. 90∘
2. 180∘
3. 270∘
4. 360∘
Thus, there are a total of 4 positions where the fan looks the same.
Step 6: Relate the order of rotational symmetry to K
The order of rotational symmetry is given as 2×K. Since we found that the order of rotational symmetry is 4, we can set up the equation:
2×K=4
Step 7: Solve for K
To find K, divide both sides of the equation by 2:
K=42=2
Final Answer
The value of K is 2.
---
Rotational symmetry refers to the number of times a shape can be rotated around a central point and still look the same within one complete turn (360 degrees).
The ceiling fan has 4 blades. We can label them as A, B, C, and D.
Since there are 4 blades, we can find the angle of rotation for each symmetry position. The angle of rotation can be calculated as:
Angle of rotation=360∘Number of blades=360∘4=90∘
- When the fan is rotated by 90∘:
- Blade A moves to the position of Blade B
- Blade B moves to the position of Blade C
- Blade C moves to the position of Blade D
- Blade D moves to the position of Blade A
- Blade A moves to the position of Blade C
- Blade B moves to the position of Blade D
- Blade C moves to the position of Blade A
- Blade D moves to the position of Blade B
- Blade A moves to the position of Blade D
- Blade B moves to the position of Blade A
- Blade C moves to the position of Blade B
- Blade D moves to the position of Blade C
- All blades return to their original positions.
From the above rotations, we can see that the fan looks the same after:
1. 90∘
2. 180∘
3. 270∘
4. 360∘
The order of rotational symmetry is given as 2×K. Since we found that the order of rotational symmetry is 4, we can set up the equation:
2×K=4
To find K, divide both sides of the equation by 2:
K=42=2
The value of K is 2.
Topper's Solved these Questions
- SYMMETRYBook:MTG IIT JEE FOUNDATIONChapter:SYMMETRYExercise:Olympiad/HOTS Corner
Explore 5 Videos
- SYMMETRYBook:MTG IIT JEE FOUNDATIONChapter:SYMMETRYExercise:Exercise (Short Answer Type)
Explore 10 Videos
- SIMPLE EQUATIONSBook:MTG IIT JEE FOUNDATIONChapter:SIMPLE EQUATIONSExercise:Olympiad /Hots Corner
Explore 18 Videos
- THE TRIANGLE AND ITS PROPERTIES Book:MTG IIT JEE FOUNDATIONChapter:THE TRIANGLE AND ITS PROPERTIES Exercise:Olympiad/Hots Corner
Explore 20 Videos
Similar Questions
Knowledge Check
A square has a rotational symmetry of order
A1B2C3D4The figure which has two lines of symmetry and rotational symmetry of order 2 is
Aa rhombusBan equilateral triangleCa semicircleDan isosceles trapeziumWhich of the following have both line symmetry and rotational symmetry of order more than 1?
AABHCCDZ
Which of the following figures have rotational symmetry of order more than 1?

View SolutionWhich of the following figures have rotational symmetry of order more than 1:
View SolutionWhich of the following figures have rotational symmetry about the marked point (*)? Also, find the order of rotational symmetry.
View SolutionFind the order of the rotational symmetry for given figure.
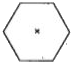
View SolutionFind the order of the rotational symmetry for given figure.
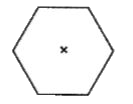
View Solution

