Find the digits from 0 to 9 which are mirror symmetric.
To find the digits from 0 to 9 that are mirror symmetric, we will analyze each digit one by one. A digit is considered mirror symmetric if it looks the same when reflected in a mirror placed vertically.
1. List the Digits: Write down all the digits from 0 to 9.
- Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
2. Check Each Digit:
- Digit 0: When reflected, 0 looks the same. Mirror symmetric.
- Digit 1: When reflected, 1 looks the same. Mirror symmetric.
- Digit 2: When reflected, 2 does not look the same. Not mirror symmetric.
- Digit 3: When reflected, 3 looks the same. Mirror symmetric.
- Digit 4: When reflected, 4 does not look the same. Not mirror symmetric.
- Digit 5: When reflected, 5 does not look the same. Not mirror symmetric.
- Digit 6: When reflected, 6 does not look the same. Not mirror symmetric.
- Digit 7: When reflected, 7 does not look the same. Not mirror symmetric.
- Digit 8: When reflected, 8 looks the same. Mirror symmetric.
- Digit 9: When reflected, 9 does not look the same. Not mirror symmetric.
3. Compile the Results: Collect all the digits that are mirror symmetric.
- Mirror Symmetric Digits: 0, 1, 3, 8
Final Answer:
The digits from 0 to 9 that are mirror symmetric are 0, 1, 3, and 8.
- Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Digit 0: When reflected, 0 looks the same. Mirror symmetric.
- Digit 1: When reflected, 1 looks the same. Mirror symmetric.
- Digit 2: When reflected, 2 does not look the same. Not mirror symmetric.
- Digit 3: When reflected, 3 looks the same. Mirror symmetric.
- Digit 4: When reflected, 4 does not look the same. Not mirror symmetric.
- Digit 5: When reflected, 5 does not look the same. Not mirror symmetric.
- Digit 6: When reflected, 6 does not look the same. Not mirror symmetric.
- Digit 7: When reflected, 7 does not look the same. Not mirror symmetric.
- Digit 8: When reflected, 8 looks the same. Mirror symmetric.
- Digit 9: When reflected, 9 does not look the same. Not mirror symmetric.
- Mirror Symmetric Digits: 0, 1, 3, 8
The digits from 0 to 9 that are mirror symmetric are 0, 1, 3, and 8.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Exercise (Subjective Problems) Long Answer Type1videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Exercise (Integer/Numerical Value Type)5videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Exercise (Subjective Problems) Very Short Answer Type14videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIO AND PROPORTIONEXERCISE - OLYMPAID/HOTS CORNER15videos
RATIO AND PROPORTION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - OLYMPIAD/HOTS CORNER20videos
UNDERSTANDING ELEMENTARY SHAPES
Similar Questions
Knowledge Check
- Question 1 - Select One
An eight digits number divisible by 9 is to the formed using digits from 0 to 9 without repeating the digits. The number of ways in which this can be done is :
A72(7!)B18(7!)C40(7!)D36(7!) - Question 2 - Select One
The number of 6 digits numbers that can be formed using the digits 0, 1, 2, 5, 7 and 9 which are divisible by 11 and no digit is repeated is
A60B72C48D36 - Question 3 - Select One
The number of six digit numbers that can be formed using the digits 0, 1, 2, 5, 7 and 9 which are divisible by 11 and no digit is repeated is :
A36B60C72D48
An eight digit number divisible by 9 is to be formed using digits from 0 to 9 without repeating the digits. The number of ways in which this can be done is: (A) 40(7!) (B) 36(7!) (C) 18(7!) (D) 72(7!)
View SolutionHow many 6-digit numbers can be formed from the digits 0,3,5,7 and 9 which are divisible by 10 and no digits is repeated?
View SolutionLet N = the number of 6 digit numbers that can be formed from the digits 0, 1, 2, 5, 7 and 9 which are divisible by 11, then 112N = _________.
View SolutionHow many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7 and 9 which are divisible by 10 and no digit is repeated ?
View SolutionIn the diagram below, the seven letters correspond to seven unique digits chosen from 0 to 9. The relationship among the digit is such that:
P.Q.R = X.Y.Z = Q.A.Y
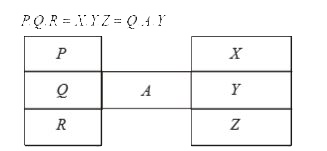
The sum of digits which are not used is:View Solution
