Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter U as U
The correct Answer is:3n
To find the rule for the number of matchsticks required to create a pattern of the letter U using matchsticks, we will follow these steps:
1. Identify the Structure of U:
- The letter U can be visualized as having two vertical sides and one horizontal bottom.
2. Count the Matchsticks for One U:
- To create one U, we need:
- 2 vertical matchsticks (one for each side)
- 1 horizontal matchstick (for the bottom)
- Therefore, the total number of matchsticks required for one U is:
2 (vertical)+1 (horizontal)=3 matchsticks
3. Establish a Variable for the Number of Us:
- Let n be the number of U's we want to create.
4. Calculate the Total Number of Matchsticks:
- If we want to make n U's, the total number of matchsticks required will be:
Total matchsticks=3×n
5. Write the Rule:
- The rule that gives the number of matchsticks required to make n U's is:
Total matchsticks=3n
Final Rule:
The rule for the number of matchsticks required to create a pattern of U's is 3n, where n is the number of U's.
---
- The letter U can be visualized as having two vertical sides and one horizontal bottom.
- To create one U, we need:
- 2 vertical matchsticks (one for each side)
- 1 horizontal matchstick (for the bottom)
- Therefore, the total number of matchsticks required for one U is:
2 (vertical)+1 (horizontal)=3 matchsticks
- Let n be the number of U's we want to create.
- If we want to make n U's, the total number of matchsticks required will be:
Total matchsticks=3×n
- The rule that gives the number of matchsticks required to make n U's is:
Total matchsticks=3n
The rule for the number of matchsticks required to create a pattern of U's is 3n, where n is the number of U's.
Topper's Solved these Questions
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - NCERT SECTION (EXERCISE - 11.2)
5 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - NCERT SECTION (EXERCISE - 11.3)
24 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - SOLVED EXAMPLES
24 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - OLYMPIAD/HOTS CORNER
10 Videos
Similar Questions
Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter T as T
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter Z as Z
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter V as V
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter E as E
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter S as S
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter A as A
View SolutionFind the rule which gives the number of matchsticks required to make thefollowing matchstick patterns. Use a variable to write the rule.(a) A pattern of letter T as(b) A pattern of letter Z as(c) A pattern of letter U as(d) A pattern of letter V as(e) A pattern of letter E as(f) A pattern of letter S as(g) A pattern of letter A as
View SolutionFind the number of matchsticks used in nth pattern.
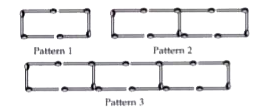
View SolutionFind the number of dots in the pattern 143 of the following pattern.

View SolutionFind the pattern followed in given figure and the number of matchsticks used in 86th figure.
View Solution
