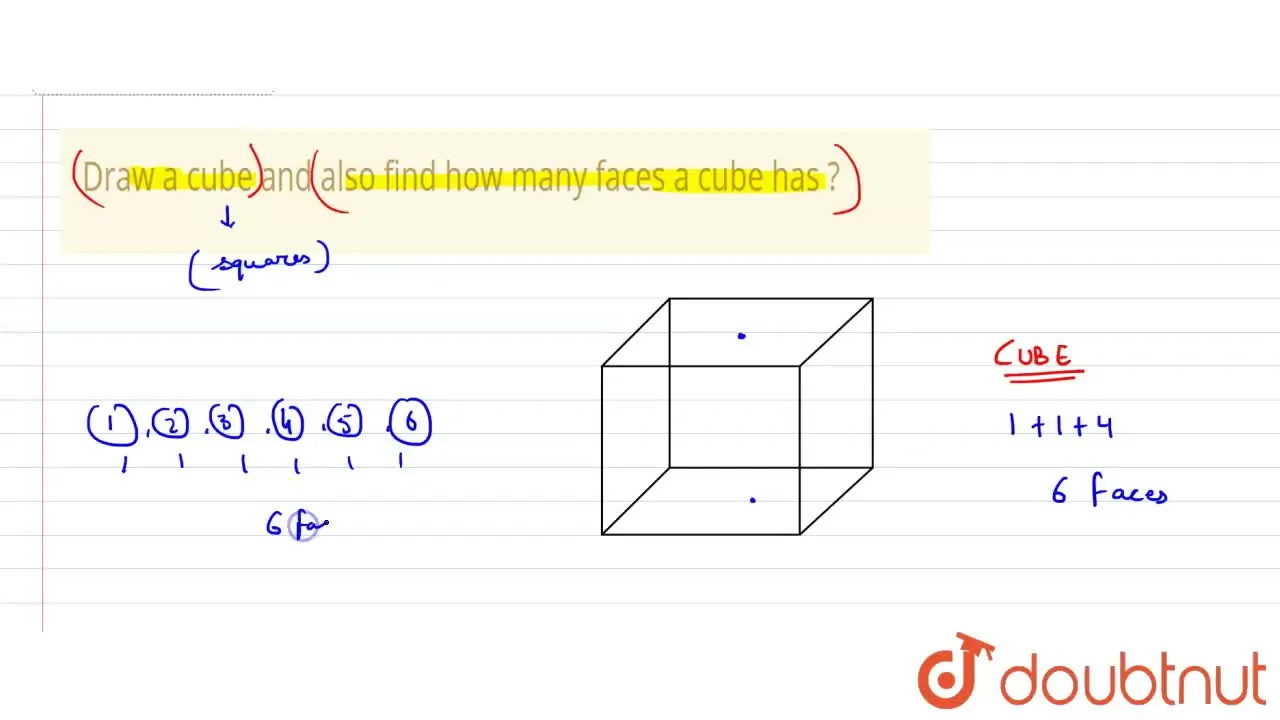
Draw a cube and also find how many faces a cube has ?
6
Related Playlists
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - EXERCISE - MULTIPLE CHOICE QUESTIONS (LEVEL - 2)15videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - EXERCISE - MULTIPLE CHOICE QUESTIONS (MATCH THE FOLLOWING)3videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - NCERT SECTION (EXERCISE 5.9)6videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Olympiad/HOTS Corner13videos
SYMMETRY
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - WHOLE NUMBERS EXERCISE - OLYMPIAD/HOTS CORNER (FILL IN THE BLANKS)5videos
WHOLE NUMBERS
Similar Questions
How many faces does a cube have?
View SolutionThe cube has how many edges?
View SolutionThe angle between diagonal of a cube and diagonal
of a face of the cube will beView SolutionA cube is 6 cm in length, breadth and height. It is painted red on two opposite faces, black on the other two opposite faces and green on the left over faces. It is then cut into 216 cubes of side 1 cm. How many small cubes have no face painted ?
View SolutionA cube is painted blue on all faces. It is cut into 125 smaller cubes of equal size.
How many cubes are painted on one face only?View SolutionA cube painted red on two adjacent faces and black on the faces opposite to the red faces and green on the remaining faces is cut into sixty- four smaller cubes of equal size. How many cubes have only one face painted:
View SolutionIn each of the following, state if the statement is true (T) or false (F) : (i)Number of faces in a cuboid and the number of faces in a cube are equal. (ii)A cube has twelve vertices.
View SolutionA compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube.
If all the atoms are removed from one of the axis passing through one of the face centers of the cube, then formula of the compound isView SolutionA compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube.
If all the atoms from the diagonals of one of the face of the cube are removed, then Zeff isView SolutionA compound formed by elements X and Y has a cubic structure in whch X atoms are at the corner of the cube and also at the face centers. Y atoms are present at the body center and at the edge center of the cube.
If all the atoms are removed from one of the plane passing through the middle of the cube, calculate total number of atoms in the cube,View Solution