Let PQ be the perpendicular to the line segment XY. Let PQ and XY intersect in the point A. What is the measure of PAY?
The correct Answer is:∠PAY=90∘
Step by step video, text & image solution for Let PQ be the perpendicular to the line segment XY. Let PQ and XY intersect in the point A. What is the measure of PAY? by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- UNDERSTANDING ELEMENTARY SHAPES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - NCERT SECTION (EXERCISE 5.6)
7 Videos
- UNDERSTANDING ELEMENTARY SHAPES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - NCERT SECTION (EXERCISE 5.7)
12 Videos
- UNDERSTANDING ELEMENTARY SHAPES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - UNDERSTANDING ELEMENTARY SHAPES EXERCISE - NCERT SECTION (EXERCISE 5.4)
19 Videos
- SYMMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Olympiad/HOTS Corner
13 Videos
- WHOLE NUMBERS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - WHOLE NUMBERS EXERCISE - OLYMPIAD/HOTS CORNER (FILL IN THE BLANKS)
5 Videos
Similar Questions
Let PQ be the perpendicular to the line segment XY. Let PQ and XY intersect in the point A. What is the measure of PAY?
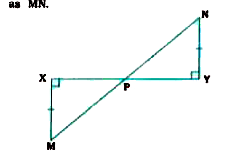
View SolutionIn the given figure, XM and YN are both < perpendicular to line segment XY and XM = YN. 4 Prove that P is the midpoint of XY as well as MN
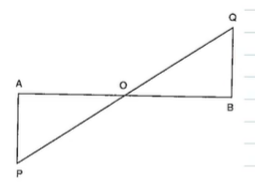
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ . Prove that O is the mid-point of line segment AB and PQ

View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ. Prove that O is the mid-point of line segment AB and PQ.
View SolutionLet P and Q be the points on the parabola y2=4x so that the line segment PQ subtends right angle If PQ intersects the axis of the parabola at R, then the distance of the vertex from R is
View SolutionDraw a line segment XY as the diameter of a circle .
View SolutionLet P be a point on the parabola y2−2y−4x+5=0, such that the tangent on the parabola at P intersects the directrix at point Q. Let R be the point that divides the line segment PQ externally in the ratio 12 : 1. Find the locus of R.
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. PS and RQ intersect at a point X on the circumference of the circle. If PQ = 9 and RS = 4, then the diameter of the circle is :
View SolutionLet PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals
View Solution
