Intensity of sound at a point is its distance from the source
directly proportional to
inversely proportional to
directly proportional to square of
inversely proportional to square of
The correct Answer is:D
To solve the question regarding the relationship between the intensity of sound and its distance from the source, we can follow these steps:
1. Understanding Intensity:
- Intensity (I) of sound is defined as the power (P) per unit area (A) through which the sound is passing.
- Mathematically, it can be expressed as:
I=PA
2. Area Calculation for a Point Source:
- For a point source emitting sound uniformly in all directions, the sound spreads out over a spherical surface.
- The area (A) of a sphere is given by the formula:
A=4πr2
- Here, r is the distance from the source.
3. Substituting Area into the Intensity Formula:
- By substituting the area of the sphere into the intensity formula, we get:
I=P4πr2
4. Analyzing the Relationship:
- From the equation I=P4πr2, we can see that intensity (I) is inversely proportional to the square of the distance (r) from the source.
- This means that as the distance from the source increases, the intensity of the sound decreases.
5. Conclusion:
- Therefore, we conclude that the intensity of sound at a point is inversely proportional to the square of its distance from the source.
Final Answer:
The intensity of sound at a point is inversely proportional to the square of its distance from the source.
---
- Intensity (I) of sound is defined as the power (P) per unit area (A) through which the sound is passing.
- Mathematically, it can be expressed as:
I=PA
- For a point source emitting sound uniformly in all directions, the sound spreads out over a spherical surface.
- The area (A) of a sphere is given by the formula:
A=4πr2
- Here, r is the distance from the source.
- By substituting the area of the sphere into the intensity formula, we get:
I=P4πr2
- From the equation I=P4πr2, we can see that intensity (I) is inversely proportional to the square of the distance (r) from the source.
- This means that as the distance from the source increases, the intensity of the sound decreases.
- Therefore, we conclude that the intensity of sound at a point is inversely proportional to the square of its distance from the source.
The intensity of sound at a point is inversely proportional to the square of its distance from the source.
Similar Questions
Knowledge Check
Two sources of sound S1andS2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0 . (a) If theta equals 45∘, what will be the intensity of sound detected at this point if one of the sources is switched off ? (b) What will be the answer of the previous part if θ=60∘ ?
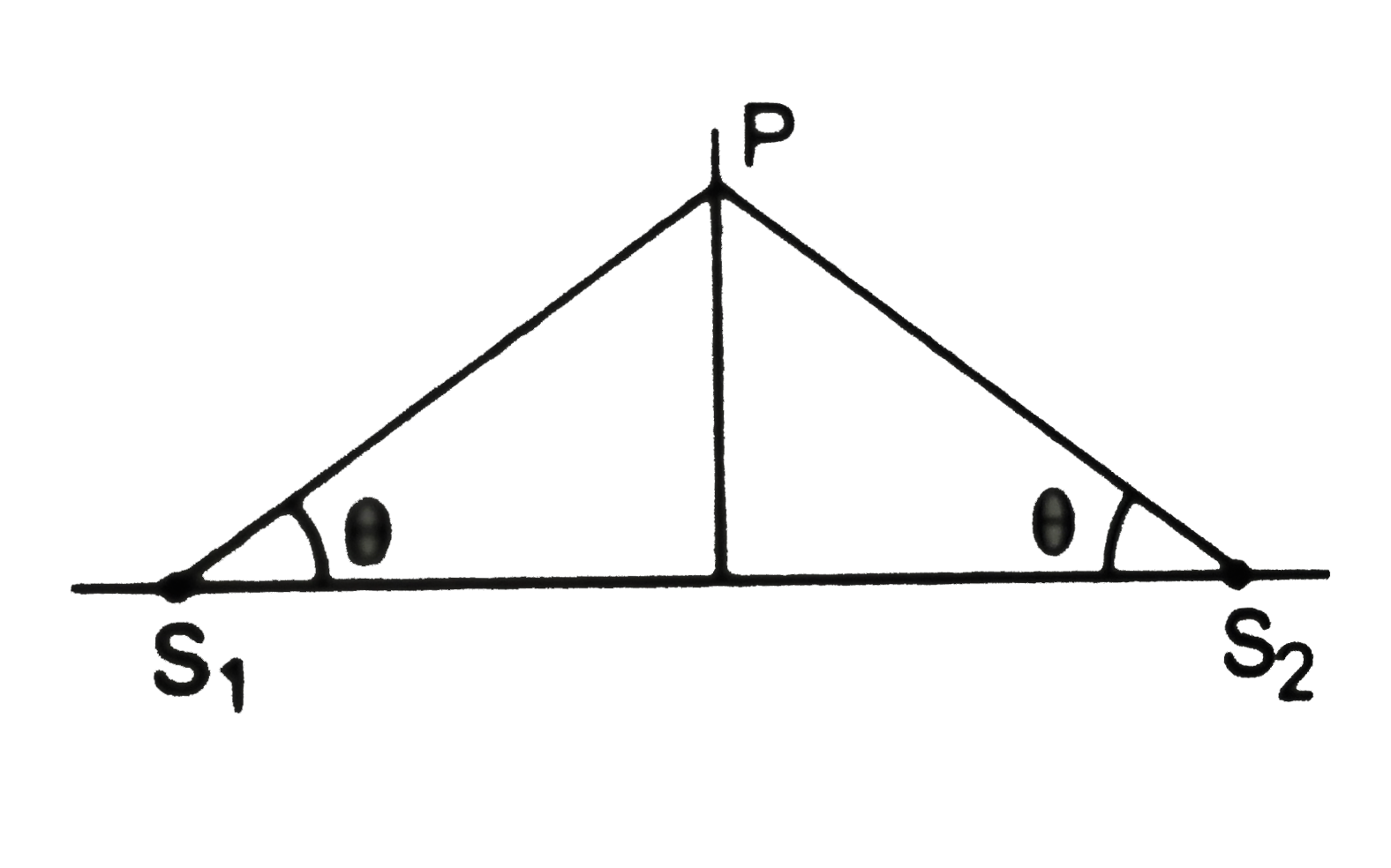 AI04,I02BI02,3I04CI04,I04DI02,I04
AI04,I02BI02,3I04CI04,I04DI02,I04A person is standing at a distance D from an isotropic point source of sound He walks 50.0 m towards the source and observes that the intensity of the sound has doubled. His initial distance D from the source is
A50√2mB50√2√2−1mC50√2−1mD100√2mThe intensity of light at a distance 'r' from the axis of a long cylindrical source is inversely proportional to 'r'
AincreasesBdecrasesCfirst increases and then decreasesDremains same
Two identical sources of sound S1andS2 produce intensity I0 at a point P equidistant from each source .
(i) Determine the intensity of each at the point P.
(ii) If the power of S1 is reduced to 64% and phase difference between the two sources is varied continuously , then determine the maximum and minimum intensities at the point P.
(iii) If the power of S1 is reduced by 64% , then determine the maximum and minimum intensities at the point P.
View SolutionSound from a point isotropic source spreads equally in all directions in homogeneous medium. Therefore its intensity decreases with square of distance from the source. When distance between observer and the source changes, apart from changes in intensity, the observer listens sound of pitch higher or lower than actual pitch depending upon the fact that the distance between the observer and source is decreasing or increasing respectively. An observer O is at a distance 2R from centre of a circle of radius R. A point isotropic sound source S moves on the circle with uniform angular velocityω=π/3 rad/s. Initially observer, source and centre of the circle are in same line.
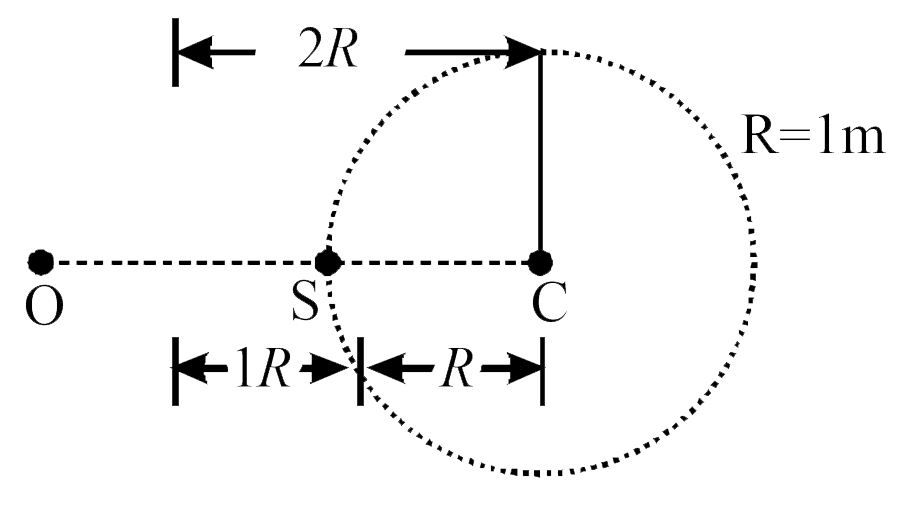
Starting from initial moment, the source moves through an angular displacement 180∘. Intensity of the sound as observed by the observer decreases by a factor of –
View SolutionSound from a point isotropic source spreads equally in all directions in homogeneous medium. Therefore its intensity decreases with square of distance from the source. When distance between observer and the source changes, apart from changes in intensity, the observer listens sound of pitch higher or lower than actual pitch depending upon the fact that the distance between the observer and source is decreasing or increasing respectively. An observer O is at a distance 2R from centre of a circle of radius R. A point isotropic sound source S moves on the circle with uniform angular velocityω=π/3 rad/s. Initially observer, source and centre of the circle are in same line.

Sound emitted by the source at two successive instants t1 and t2 has minimum and maximum observed pitch respectively, then –
View SolutionIn Youngsdoub≤slitexperiment,thephased⇔erentbetweentwocoherentsourcesofequal∫ensityisπ3.The∫ensityatap∮whichisatequaldistanceomthetwoslitsis(l_@) is maximum intensity)
View SolutionIntensity of sound at a point is its distance from the source
View Solution