What is the speed of light in diamond if its refractive index is 2.41 ?
To find the speed of light in diamond given its refractive index, we can follow these steps:
1. Understand the Concept of Refractive Index:
The refractive index (n) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in that medium (v). The formula is:
n=cv
2. Identify Given Values:
- Refractive index of diamond (n) = 2.41
- Speed of light in vacuum (c) = 3×108 meters per second.
3. Rearrange the Formula:
To find the speed of light in diamond (v), we can rearrange the formula:
v=cn
4. Substitute the Values:
Now, substitute the known values into the rearranged formula:
v=3×108 m/s2.41
5. Perform the Calculation:
Calculate the value:
v≈3×1082.41≈1.24×108 m/s
6. Final Answer:
Therefore, the speed of light in diamond is approximately:
v≈1.24×108 m/s
The refractive index (n) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in that medium (v). The formula is:
n=cv
- Refractive index of diamond (n) = 2.41
- Speed of light in vacuum (c) = 3×108 meters per second.
To find the speed of light in diamond (v), we can rearrange the formula:
v=cn
Now, substitute the known values into the rearranged formula:
v=3×108 m/s2.41
Calculate the value:
v≈3×1082.41≈1.24×108 m/s
Therefore, the speed of light in diamond is approximately:
v≈1.24×108 m/s
Similar Questions
Knowledge Check
Light travels with a speed of 2×108ms−1 in crown glass of refractive index 1.5. What is the speed of light in dense flint glass of refractive index 1.8 ?
A1.33×108ms−1B1.67×108ms−1C2.0×108ms−1D3.0×108ms−1The speed of light in air is 3×108m/s. What will be its speed in diamond whose refractive index is 2.4
A3×108m/sB332m/sC1.25×108m/sD7.2×108m/sThe speed of light in a medium of refractive index 1.5 is ________.
A1.5×108m/sB3.0×108m/sC2.0×108m/sD1.2×108m/s
(a) What is the speed of light in water of refractive index 4/3?
(b) Light travels in a medium with a velocity of 2×108m/s. What is refractive index of the medium?
View SolutionThe refractive index of glycerine is 1.46. What is the speed of light in air if its speed in glycerine is 2.05x108m/s ?
View SolutionDefine refractive index of a tranparent medium . The speed of light in a medium of absolute refractive index 1.5 is 2×108ms−1 . What is the speed of light in vacuum ?
View SolutionThe table below gives the refractive index of a few materials and the speed of light in that medium
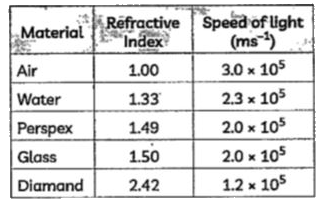
The speed of light in a medium 'A' having refractive index 2 .00 will be
View SolutionLight enters from air to diamond with refractive index 2.42 What is the speed of light in diamond ? Given, speed light in air is 3×108ms−1.
View Solution
