A uniform meter scale is kept in equilibrium when supported at the 60 cm mark and a mass weight of the scale is greater than, less than or equal to the weight of mass M.

Video Solution

Text Solution

Verified by Experts

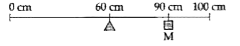
The weight of the scale W will act from 50 cm mark. By principle of moments,
$Load \times load arm = Effort \times effort arm$
$W \times (60 - 50) = M \times (90 - 60)$
$\Rightarrow W \times 10 M \times 30$
$\Rightarrow W = 3 M$
Hence weight of scale is three times the mass M.

|

Updated on:21/07/2023

Class 8 PHYSICS SIMPLE MACHINES

Similar Questions

Knowledge Check

Question 1 - Select One
If mass of the planet is $10 %$ less than that of the earth and radius of the planet is $20 %$ greater than that of the earth then the weight of $40 k g$ person on that planet is
A $10 k g w t$
B $25 k g w t$
C $40 k g w t$
D $60 k g w t$
Question 2 - Select One
An uniform metre scale of weight $50 g$ is balanced at $60 c m$ mark, when a weight of $15 g$ is suspended at $10 c m$ mark. Where must a weight $100 g$ be suspended to balance metre scale.
A $72.5 c m$
B $70 c m$
C $71.5 c m$
D $74.5 c m$
Question 3 - Select One
A uniform meter scale balances at the 40 cm mark when weights of 10g and 20g are suspended from the 10cm and 20cm marks. The weight of the metre scale is
A50 g
B60 g
C70 g
D80 g

Recommended Questions

Home
Ask Doubt
Profile