When oil and water are mixed together, the two substances separate and the oil floats to the top. How does the density of oil compare with the density of water?
To determine how the density of oil compares with the density of water, we can follow these steps:
1. Understanding the Scenario: When oil and water are mixed, they do not combine and instead separate into two layers, with oil floating on top of water.
2. Observing the Behavior of Oil and Water: The fact that oil floats on water indicates a specific relationship between their densities.
3. Applying the Principle of Density: The principle of flotation states that an object will float if its density is less than the density of the liquid it is in. Conversely, if the density is greater, the object will sink.
4. Identifying the Densities: In this case, the oil is the object and water is the liquid. Since oil floats on water, we can conclude that the density of oil must be less than the density of water.
5. Conclusion: Therefore, we can definitively state that the density of oil is less than the density of water.
Final Answer:
The density of oil is less than the density of water.
---
The density of oil is less than the density of water.
Similar Questions
Knowledge Check
Oil and paint when mixed with water.
Asink in waterBfloat on waterCdissolve in waterDmake a layer in the centre of water.Oil and water _____ not mix.
AdoesBhadCdoDisThe process used to separate oil and water is
AdistillationBsublimationCextractionDchromatography
Oil mixes with water.
View SolutionFor the arrangement shown in the figure, what is the density of oil?
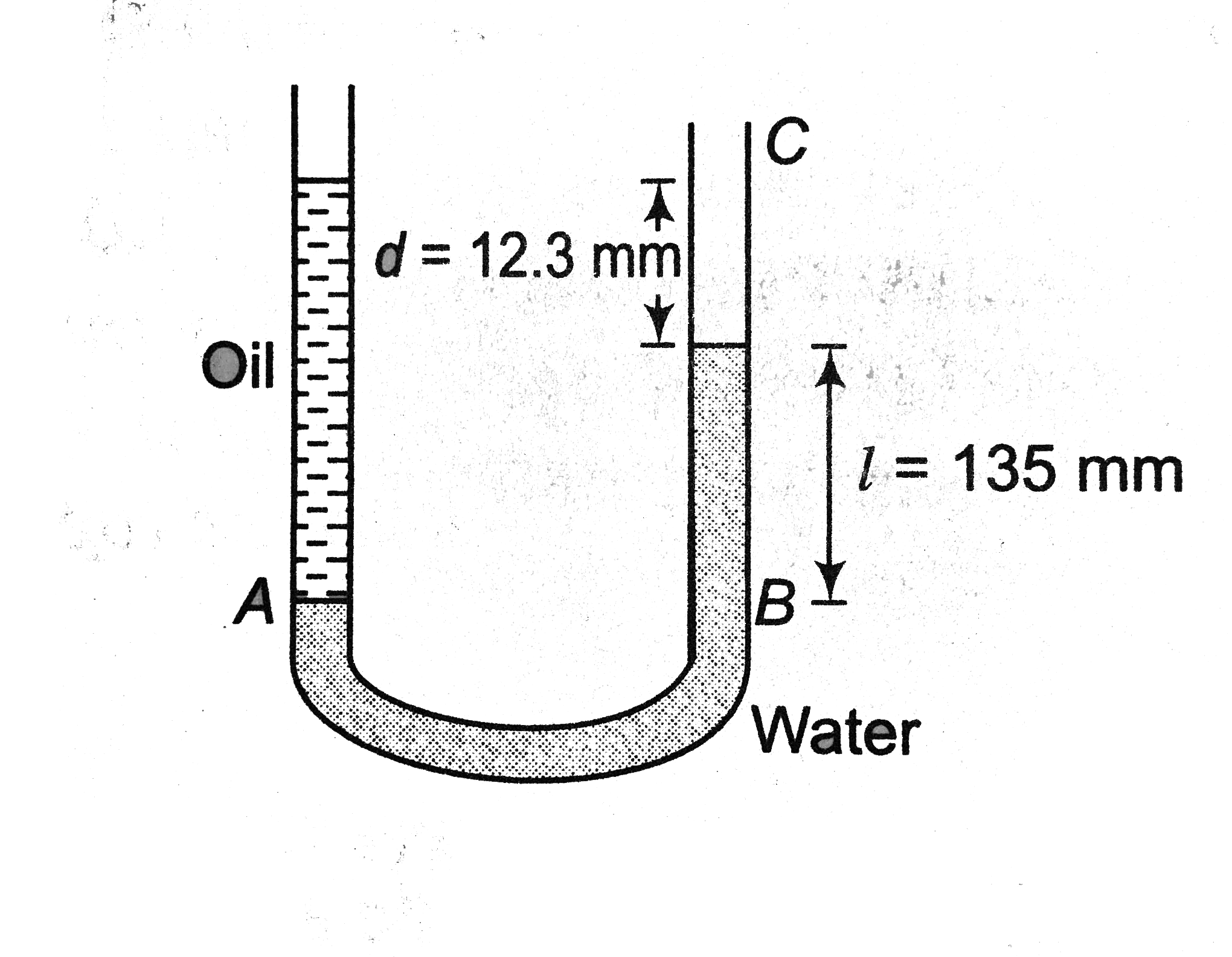 .
.
View SolutionName the apparatus you would use to separate oil from water.
View SolutionA density bottle weighs 120 g and 100 g when filled completely with oil ad water, respectively. If the weight of a empty density bottle is 40g, then arrange the following steps in sequence meant to solve the problem to get the density of oil
(A). The density of the oil
D=Mass of the oilWeight of the water=Mass of the oilMass of the water
=Weighht of oilWeight of the water=W3−W1W2−W1
(B). Let the weight of the bottle +oil=W3=120g
and the weight of the bottle+water =W2
100g, where bottle is completely filled with liquid, i.e., oil or water.
(C). Let the weight of the empty bottle=W1=40g
(D). The the weight of the oil ad water would be equal to (W3−W1)and(W2−W1), respectively.
View SolutionA density bottle weighs 120 g and 100 g when filled completely with oil ad water, respectively. If the weight of a empty density bottle is 40g, then arrange the following steps in sequence meant to solve the problem to get the density of oil
(A). The density of the oil
D=Mass of the oilWeight of the water=Mass of the oilMass of the water
=Weighht of oilWeight of the water=W3−W1W2−W1
(B). Let the weight of the bottle +oil=W3=120g
and the weight of the bottle+water =W2
100g, where bottle is completely filled with liquid, i.e., oil or water.
(C). Let the weight of the empty bottle=W1=40g
(D). The the weight of the oil ad water would be equal to (W3−W1)and(W2−W1), respectively.
View Solution
