A mass of 4 kg originally at rest is pulled by a string along a smooth horizontal surface. The force of 15 N is maintained until the mass undergoes a displacement of 20m. at which stage the mass is allowed to keep moving at constant velocity.
How much work is done by the force ?
To solve the problem, we need to calculate the work done by the force acting on the mass. The formula for work done (W) is given by:
W=F×d
where:
- W is the work done,
- F is the force applied, and
- d is the displacement.
Now, let's go through the solution step by step:
Step 1: Identify the values given in the problem
- The force F=15N
- The displacement d=20m
Step 2: Use the work done formula
We can substitute the values of force and displacement into the work done formula:
W=F×d
Step 3: Substitute the values
Now, substituting the known values into the equation:
W=15N×20m
Step 4: Calculate the work done
Now, we perform the multiplication:
W=300N⋅m
Since 1N⋅m=1J (Joule), we can conclude:
W=300J
Final Answer
The work done by the force is 300J.
---
- W is the work done,
- F is the force applied, and
- d is the displacement.
- The force F=15N
- The displacement d=20m
We can substitute the values of force and displacement into the work done formula:
Now, substituting the known values into the equation:
Now, we perform the multiplication:
The work done by the force is 300J.
Topper's Solved these Questions
- WORK AND ENERGYBook:S CHAND IIT JEE FOUNDATIONChapter:WORK AND ENERGYExercise:SELF ASSESSMENT SHEET-3
Explore 27 Videos
- WORK AND ENERGYBook:S CHAND IIT JEE FOUNDATIONChapter:WORK AND ENERGYExercise:SELF ASSESSMENT SHEET-3
Explore 27 Videos
- MEASUREMENT AND MOTIONBook:S CHAND IIT JEE FOUNDATIONChapter:MEASUREMENT AND MOTIONExercise:Self Assessment Sheet -1 (a)
Explore 14 Videos
Similar Questions
A mass of 4 kg originally at rest is pulled by a string along a smooth horizontal surface. The force of 15 N is maintained until the mass undergoes a displacement of 20m. at which stage the mass is allowed to keep moving at constant velocity.
What would be the velocity of the mass at the end of 20 m ?
View SolutionFigure shows four blocks that are being pulled along a smooth horizontal surface.The masses of the blocks and tension in one cord are given.The pulling force F is
View Solution
Knowledge Check
Work done by the gravitational force on a body of mass ''m'' moving on a smooth horizontal surface through a distance 's' is
AmgsB−mgsC0D2mgsA body of mass 1 kg is initially at rest is moved by a horizontal force of 0.5 Nona smooth frictionless table. The value of work done by this force in 10 s is
A10.9 JB13.1 JC14.3 JD12.5 JA force of 75 N is applied to a block of mass 25 kg, resting on a smooth horizontal surface. In how much time, the block will acquire a speed of 12 m/s?
A1 secB2secC4 secD8 sec
Three blocks of masses m1=10kg,m2=20kg,m3=30kg are connected by strings on smooth horizontal surface and pulled by a force of 60 N. Find the acceleration of the system and tensions in the string.

View SolutionAn object of mass m is moving with a constant velocity υ How much work should be done on the object in order to bring the object to rest ?
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.

View SolutionA body of mass 25 kg is at rest on a horizontal surface. Minimum horizontal force required to just start the motion is 73.5 N and a force of 49 N is needed to keep the body moving with a constant velocity. What is the coefficient of static friction?
View SolutionA block of mass 20 kg is moving on a smooth surface by pulling through a light string of tension 10√2 N. Find the work done by string on the block for a displacement of 2 m along the surface.
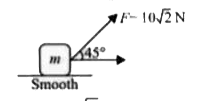
View Solution