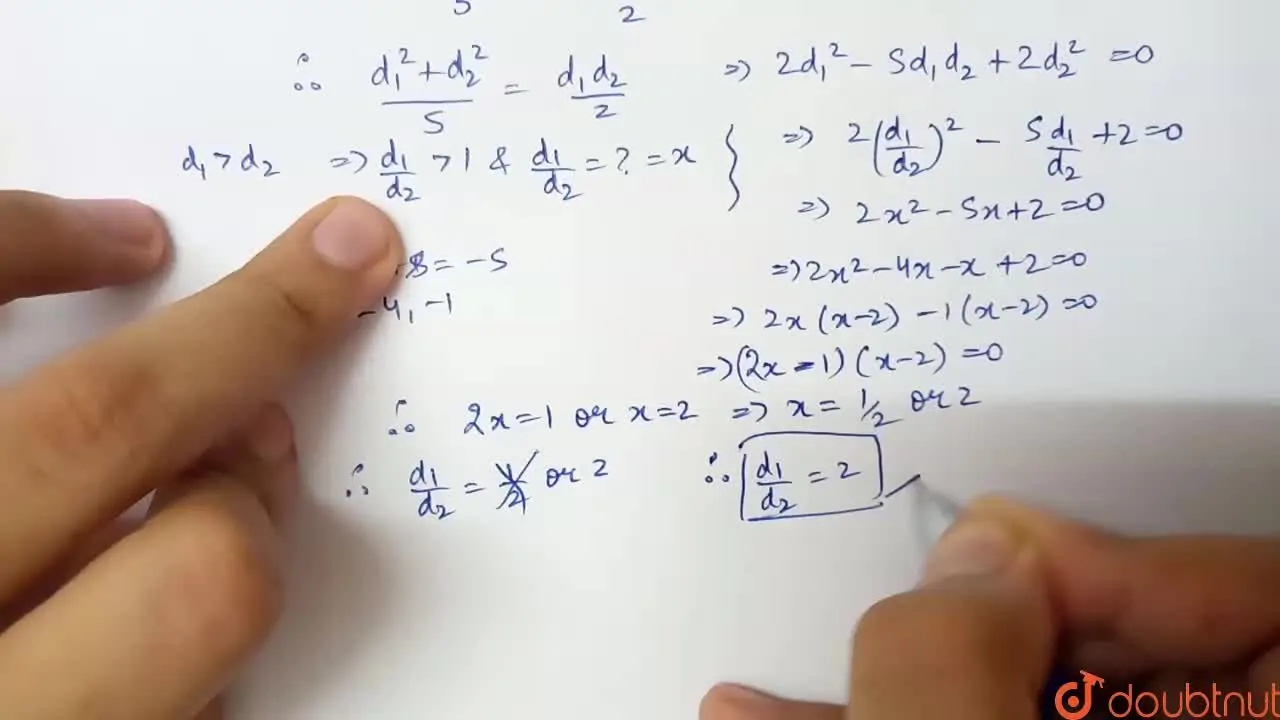A rhombus has an area equal to one-fifth the sum of the areas of the squares built on its four sides. The ratio of the long diagonal to the short diagonal is:
2+√3
2−√3
12
2
The correct Answer is:D
Step by step video, text & image solution for A rhombus has an area equal to one-fifth the sum of the areas of the squares built on its four sides. The ratio of the long diagonal to the short diagonal is: by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Related Playlists
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS EXERCISE - Question Bank-2625videos
AREA AND PERIMETER OF RHOMBUS, TRAPEZIUM AND POLYGONS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AREA AND PERIMETER OF RECTANGLE, SQUARE, PARALLELOGRAM, TRIANGLE AND CIRCLESEXERCISE - Question Bank - 25 (M.C.Q)15videos
AREA AND PERIMETER OF RECTANGLE, SQUARE, PARALLELOGRAM, TRIANGLE AND CIRCLES
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET10videos
AVERAGE
Similar Questions
A rhombus has an area equal to one-fifth the sum of the areas of the squares built on its four sides. The ratio of the long diagonal to the short diagonal is:
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
View SolutionThe ratio of the area of a square to that of the square drawn on its diagonal is :
View SolutionIf one of the diagonals of a rhombus is equal to its side, then the diagonals of the rhombus are in the ratio
View SolutionIf one of the diagonals of a rhombus is equal to its side, then the diagonals of the rhombus are in the ratio
View SolutionThe length of each side of a rhombus is equal to the length of the side of a square whose diagonal is 40√2 cm. If the length of the diagonals of the rhombus are in the ratio 3:4. then its area (in cm2) is
View SolutionThe ratio of the area of a square to that of the square drawn on its diagonal is:
View SolutionThe ratio of the area of a square to that of the square drawn on its diagonal is:
View SolutionThe ratio of the area of a square to that of the square drawn on its diagonal is:
View SolutionThe length of one diagonal of a rhombus is 80% of the other diagonal. The area of the rhombus is how many times the square of the length of the other diagonal? 45 (b) 25 (c) 34 (d) 14
View Solution