BC, AB and AC are tangents to the circle at D, E and F respectively. ∠EBD=x∘,∠FCD=y∘. Then ∠ EDF equals
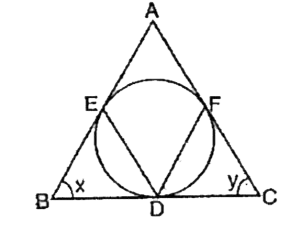
x + y
x2−y
90∘−(x+y)
x+y2
The correct Answer is:D
Step by step video, text & image solution for BC, AB and AC are tangents to the circle at D, E and F respectively. angle EBD = x^(@), angle FCD = y^(@). Then angle EDF equals by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - SELF ASSESSMENT SHEET - 24
10 Videos
- AVERAGEBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - AVERAGEEXERCISE - SELF ASSESSMENT SHEET
10 Videos
- CO-ORDINATE GEOMETRYBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Self Assessment Sheet
10 Videos
Similar Questions
In Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View Solution
Knowledge Check
In the figure , if AD, AE and BC are tangent to the circle at D,E and F , respectively , then
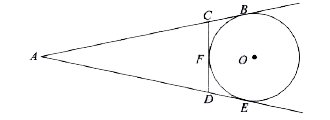 AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CA
AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CAIn the given figure, O is the centre of the circle . AC and AB are the tangents to the circular at points P and Q , respectively. Also ∠RPC=55∘and∠RQB=60∘ then ∠PRQand∠QAP are, respectively .
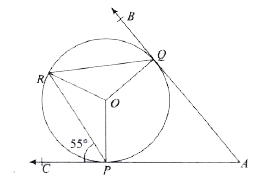 A50∘B60∘C30∘D40∘
A50∘B60∘C30∘D40∘In △ABC ,AB=AC , ∠B=40∘ Then ∠C is equal to
A50∘B40∘C80∘D140∘
In a △ABC, ∠A=52∘. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBD and ∠BCE meet at point O, then ∠BOC is equal to:
△ABC में ∠A=52∘ है। इनकी भुजाएं AB और AC क्रमशः D और E तक बढाई जाती है। अगर ∠CBD और ∠BCE समदूविभाजक बिंदु O पर मिलते हैं, तो ∠BOC बराबर हैः
View SolutionThe sides AC,BC and AB of a triangle ABC are tangents to its incircle at D,E and F, respectively. Point D lies on the hypotenuse AC such that D is the circumcentre of the triangle ABC. Find EF:AC.
View SolutionIn the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
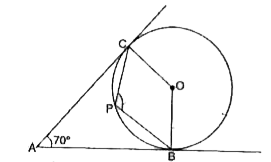
View SolutionIn the diagram, A, B, C, D, E are points on the circle. AB||DC, ∠ADE=39∘and∠ABC=62∘. Then the values of x and y respectively are :
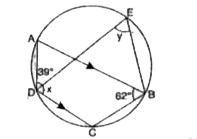
View SolutionThe sides BC,CA and AB of △ABC have been produced to D, E and F respectively as shown in the figure, forming exterior angles ∠ACD,∠BAEand∠CBF. Then, ∠ACD+∠BAE+∠CBF is equal to
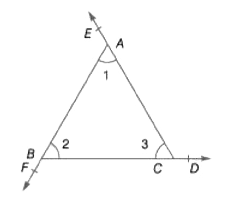
View Solution
