The inequality , where x is an integer can be represented on the number line as:




The correct Answer is:C
To solve the inequality −1≤2x+4<5 where x is an integer, we will break it down into steps.
Step 1: Split the Compound Inequality
We can rewrite the compound inequality as two separate inequalities:
1. 2x+4≥−1
2. 2x+4<5
Step 2: Solve the First Inequality
Starting with the first inequality:
2x+4≥−1
Subtract 4 from both sides:
2x≥−1−4
2x≥−5
Now, divide both sides by 2:
x≥−52
This simplifies to:
x≥−2.5
Step 3: Solve the Second Inequality
Now, we solve the second inequality:
2x+4<5
Subtract 4 from both sides:
2x<5−4
2x<1
Now, divide both sides by 2:
x<12
Step 4: Combine the Results
Now we have two inequalities:
1. x≥−2.5
2. x<0.5
Step 5: Determine Integer Solutions
Since x must be an integer, we consider the integers that satisfy both inequalities:
- The integers greater than or equal to −2.5 are −2,−1,0.
- The integers less than 0.5 are −2,−1,0.
Thus, the integer solutions are:
x=−2,−1,0
Step 6: Represent on the Number Line
On the number line, we would represent the integers −2, −1, and 0 as points marked on the line.
Final Answer
The integer solutions to the inequality −1≤2x+4<5 are −2, −1, and 0.
---
We can rewrite the compound inequality as two separate inequalities:
1. 2x+4≥−1
2. 2x+4<5
Starting with the first inequality:
2x+4≥−1
Subtract 4 from both sides:
2x≥−1−4
2x≥−5
Now, divide both sides by 2:
x≥−52
This simplifies to:
x≥−2.5
Now, we solve the second inequality:
2x+4<5
Subtract 4 from both sides:
2x<5−4
2x<1
Now, divide both sides by 2:
x<12
Now we have two inequalities:
1. x≥−2.5
2. x<0.5
Since x must be an integer, we consider the integers that satisfy both inequalities:
- The integers greater than or equal to −2.5 are −2,−1,0.
- The integers less than 0.5 are −2,−1,0.
x=−2,−1,0
On the number line, we would represent the integers −2, −1, and 0 as points marked on the line.
The integer solutions to the inequality −1≤2x+4<5 are −2, −1, and 0.
Topper's Solved these Questions
- LINEAR INEQUALITIESBook:S CHAND IIT JEE FOUNDATIONChapter:LINEAR INEQUALITIESExercise:SELF ASSESMENT SHEET -13
Explore 10 Videos
- LINEAR INEQUALITIESBook:S CHAND IIT JEE FOUNDATIONChapter:LINEAR INEQUALITIESExercise:SELF ASSESMENT SHEET -13
Explore 10 Videos
- LINEAR EQUATIONS IN ONE VARIABLE (REVISION)Book:S CHAND IIT JEE FOUNDATIONChapter:LINEAR EQUATIONS IN ONE VARIABLE (REVISION)Exercise:Self Assessment Sheet
Explore 10 Videos
- MATRICES Book:S CHAND IIT JEE FOUNDATIONChapter:MATRICES Exercise:UNIT TEST -2
Explore 20 Videos
Similar Questions
Knowledge Check
The inequality |3−p|−4<1 can be represented on the number line as:
A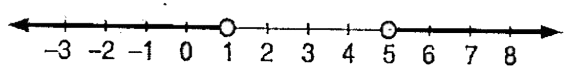 B
B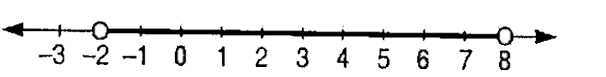 C
C D
D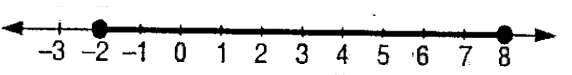
Solve the inequation 12x<50 If (i) x ∈ Z (ii) x ∈ R and represent the solution on the number line
View SolutionSolve the inequation 2x+5>−5x+12 If x ∈ R and represent the solution on the number line
View SolutionSolve the inequation 5x−2≥3x−1 If x ∈ R and represent the solution on the number line
View SolutionSolve the inequation 3x−2<5 If (i) x∈ N (ii) x ∈ R and represent the solution on the number line
View SolutionSolve the inequation −3≤3−2x<9,x∈R. Represent the solution set on the real line.
View SolutionSolve the inequation 30x<200 If (i) x ∈ Z (ii) x ∈N and represent the solution on the number line
View SolutionSolve the inequation 6x−5≤7 If (i) x ∈ I (ii) x ∈ R and represent the solution on the number line
View Solution