In a group of 15, 7 have studied German, 8 have studied French and 3 have not studied either . The Venn diagram showing the number of students who have studied both is
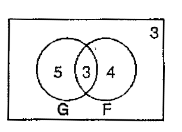
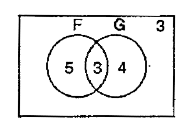
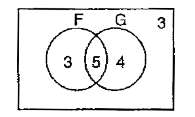
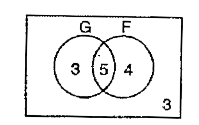
The correct Answer is:B
Step by step video, text & image solution for In a group of 15, 7 have studied German, 8 have studied French and 3 have not studied either . The Venn diagram showing the number of students who have studied both is by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETSBook:S CHAND IIT JEE FOUNDATIONChapter:SETSExercise:Self Assessment Sheet
Explore 10 Videos
- SETSBook:S CHAND IIT JEE FOUNDATIONChapter:SETSExercise:Self Assessment Sheet
Explore 10 Videos
- RATIO AND PROPORTION Book:S CHAND IIT JEE FOUNDATIONChapter:RATIO AND PROPORTION Exercise:SELF ASSESSMENT SHEET - 15
Explore 10 Videos
- SIMPLE INTEREST Book:S CHAND IIT JEE FOUNDATIONChapter:SIMPLE INTEREST Exercise:Self Assessment Sheet
Explore 10 Videos
Similar Questions
Give the example of X- monosomy you have studied.
View SolutionIn a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry , 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects.
View Solution
Knowledge Check
Radioactive tracer studies with .14C have shown that
APhloem transports organic nutrientsBPhloem transports inorganic nutrientsCXylem transports inorganic nutrientsDXylem transport organic nutrients.Study the Pie chart carefully and answer the questions.
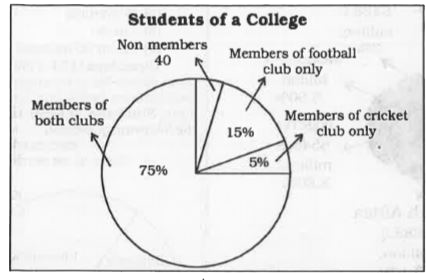
The number of students who are members of both the club is :A500B650C550D600Study the given Venn diagram.

The centre point representsABaking of cakeBMaking a lemonadeCFormation of rocksDExplosion of dynamite.
Study the given Venn diagram and fill in the blanks.
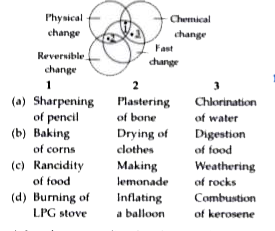
View SolutionFill in the blank with correct form of verb.
Had the teacher not come, the students ……… (would have studied/studied)
View SolutionWrite the formula for Inclusion-Exclusion principle and suppose that 100 of 120 mathematics students was college take at least one of the languages French, German and Russian. Also suppose 65 study French 45study German, 42 study Russian, 20 study French and German, 25 study French and Russian 15 study German and Russian. Find the number of student studying all subjects. Also find studying exactly one subject.
View SolutionStudy the given Venn diagram carefully.
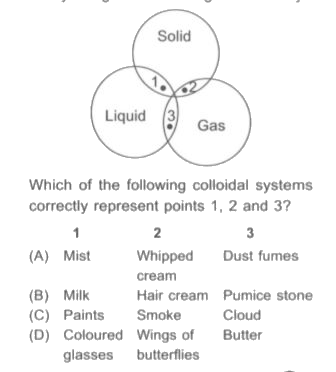
View SolutionStudy the given Venn diagram carefully. The centre point X represents
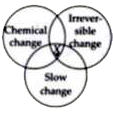
View Solution
