A right angled isosceles triangle is inscribed in a circle of radius r. What is the area of the remaining portion of the circle ?
πr22
(π−12)r2
(π−1)r2
(π−2)r2
The correct Answer is:C
To find the area of the remaining portion of a circle when a right-angled isosceles triangle is inscribed in it, we can follow these steps:
1. Identify the Circle's Area:
The area of a circle is given by the formula:
Area of Circle=πr2
where r is the radius of the circle.
2. Determine the Triangle's Side Length:
Since the triangle is a right-angled isosceles triangle inscribed in the circle, we can denote the lengths of the equal sides of the triangle as A. The hypotenuse of the triangle will be the diameter of the circle, which is 2r.
3. Apply the Pythagorean Theorem:
According to the Pythagorean theorem:
(2r)2=A2+A2
Simplifying this gives:
4r2=2A2
Dividing both sides by 2:
2r2=A2
Taking the square root of both sides:
A=r√2
4. Calculate the Area of the Triangle:
The area of a triangle is given by:
Area of Triangle=12×base×height
For our isosceles triangle, both the base and height are equal to A:
Area of Triangle=12×A×A=12×(r√2)×(r√2)=12×2r2=r2
5. Find the Remaining Area:
Now, we can find the area of the remaining portion of the circle by subtracting the area of the triangle from the area of the circle:
Remaining Area=Area of Circle−Area of Triangle
Substituting the values we calculated:
Remaining Area=πr2−r2=(π−1)r2
Final Answer:
The area of the remaining portion of the circle is:
Remaining Area=(π−1)r2
The area of a circle is given by the formula:
Area of Circle=πr2
where r is the radius of the circle.
Since the triangle is a right-angled isosceles triangle inscribed in the circle, we can denote the lengths of the equal sides of the triangle as A. The hypotenuse of the triangle will be the diameter of the circle, which is 2r.
According to the Pythagorean theorem:
(2r)2=A2+A2
Simplifying this gives:
4r2=2A2
Dividing both sides by 2:
2r2=A2
Taking the square root of both sides:
A=r√2
The area of a triangle is given by:
Area of Triangle=12×base×height
For our isosceles triangle, both the base and height are equal to A:
Area of Triangle=12×A×A=12×(r√2)×(r√2)=12×2r2=r2
Now, we can find the area of the remaining portion of the circle by subtracting the area of the triangle from the area of the circle:
Remaining Area=Area of Circle−Area of Triangle
Substituting the values we calculated:
Remaining Area=πr2−r2=(π−1)r2
The area of the remaining portion of the circle is:
Remaining Area=(π−1)r2
Topper's Solved these Questions
- CIRCUMFERENCE AND AREA OF A CIRCLE Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCUMFERENCE AND AREA OF A CIRCLE Exercise:SELF ASSESSMENT SHEET - 22
Explore 10 Videos
- CIRCUMFERENCE AND AREA OF A CIRCLE Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCUMFERENCE AND AREA OF A CIRCLE Exercise:SELF ASSESSMENT SHEET - 22
Explore 10 Videos
- CIRCLES Book:S CHAND IIT JEE FOUNDATIONChapter:CIRCLES Exercise:UNIT TEST
Explore 20 Videos
- DATA HANDLING Book:S CHAND IIT JEE FOUNDATIONChapter:DATA HANDLING Exercise:Self Assessment Sheet - 24
Explore 10 Videos
Similar Questions
Knowledge Check
Area of an equilateral triangle inscribed in a circle of radius a is
A√3a2/4Bπa2/3C3√3a2/4D√3πa2/4A right angled isosceles triangle is inscribed in a semi-circle of radius 7 cm. The area enclosed by the semi-circle but exterior to the triangle is
A14cm2B28cm2C44cm2D68cm2In the figure below, the square JKLM is inscribed within a circle and ΔJMN is a right-angled isosceles triangle. The point marked O is the centre of the circle.
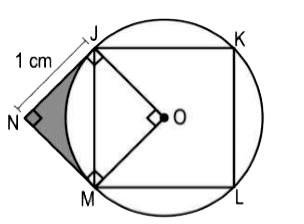
What is the area of the shaded part of the figure?A(π4−12)cm2B(π−12)cm2C(1−π4)cm2D(1−π)cm2
An equilateral triangle is inscribed in a circle of radius 'r' units. The area of shaded region is
View SolutionABC is an equilateral triangle inscribed in a circle of radius 4 cm. Find the area of the shaded portion.

View SolutionIf an isosceles triangle ABC in which AB=AC=6cm is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionThe area of an equilateral triangle inscribed in a circle of radius 4cm, is
View SolutionIf a triangle is inscribed in a circle of radius r , then which of the following triangle can have maximum area
View Solution
