Two lines in a plane are cut by a transversal .Which condition does NOT imply that the two lines are parallel ?
A pair of alternate interior angles are congruent .
A pair of co- interior angles are supplementary .
A pair of corresponding angles are congruent .
A pair of alternate exterior angles are complementary .
The correct Answer is:D
To solve the question, we need to identify which condition does NOT imply that two lines cut by a transversal are parallel. Let's analyze the conditions one by one.
1. Understanding the Terms:
- Transversal: A line that intersects two or more lines in a plane.
- Parallel Lines: Two lines that never meet and are always the same distance apart.
- Angles: Various types of angles formed when a transversal cuts two lines, such as alternate interior angles, co-interior angles, corresponding angles, and alternate exterior angles.
2. Condition 1: Alternate Interior Angles are Congruent:
- If a pair of alternate interior angles are equal, then the two lines are parallel.
- Example: If ∠AGH = ∠GHD, then AB || CD.
- Conclusion: This condition implies that the lines are parallel.
3. Condition 2: Co-Interior Angles are Supplementary:
- If a pair of co-interior angles are supplementary (sum to 180 degrees), then the two lines are parallel.
- Example: If ∠BGH + ∠GHD = 180°, then AB || CD.
- Conclusion: This condition implies that the lines are parallel.
4. Condition 3: Corresponding Angles are Congruent:
- If a pair of corresponding angles are equal, then the two lines are parallel.
- Example: If ∠EGB = ∠GHD, then AB || CD.
- Conclusion: This condition implies that the lines are parallel.
5. Condition 4: Alternate Exterior Angles are Complementary:
- If a pair of alternate exterior angles are complementary (sum to 90 degrees), this does NOT imply that the two lines are parallel.
- Example: If ∠AGE + ∠FHD = 90°, it does not guarantee that AB || CD.
- Conclusion: This condition does NOT imply that the lines are parallel.
Final Answer:
The condition that does NOT imply that the two lines are parallel is: A pair of alternate exterior angles are complementary.
---
- Transversal: A line that intersects two or more lines in a plane.
- Parallel Lines: Two lines that never meet and are always the same distance apart.
- Angles: Various types of angles formed when a transversal cuts two lines, such as alternate interior angles, co-interior angles, corresponding angles, and alternate exterior angles.
- If a pair of alternate interior angles are equal, then the two lines are parallel.
- Example: If ∠AGH = ∠GHD, then AB || CD.
- Conclusion: This condition implies that the lines are parallel.
- If a pair of co-interior angles are supplementary (sum to 180 degrees), then the two lines are parallel.
- Example: If ∠BGH + ∠GHD = 180°, then AB || CD.
- Conclusion: This condition implies that the lines are parallel.
- If a pair of corresponding angles are equal, then the two lines are parallel.
- Example: If ∠EGB = ∠GHD, then AB || CD.
- Conclusion: This condition implies that the lines are parallel.
- If a pair of alternate exterior angles are complementary (sum to 90 degrees), this does NOT imply that the two lines are parallel.
- Example: If ∠AGE + ∠FHD = 90°, it does not guarantee that AB || CD.
- Conclusion: This condition does NOT imply that the lines are parallel.
The condition that does NOT imply that the two lines are parallel is: A pair of alternate exterior angles are complementary.
Topper's Solved these Questions
- LINES AND ANGLES Book:S CHAND IIT JEE FOUNDATIONChapter:LINES AND ANGLES Exercise:QUESTIONS BANK
Explore 22 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBook:S CHAND IIT JEE FOUNDATIONChapter:LINEAR EQUATIONS IN ONE VARIABLEExercise:Unit Test -2
Explore 20 Videos
- NUMBERSBook:S CHAND IIT JEE FOUNDATIONChapter:NUMBERSExercise:SELF ASSESSMENT SHEET-1
Explore 10 Videos
Similar Questions
Angles made by a transversal with two lines - interior angles.
View SolutionIn the figure, which of the two lines are parallel and why ?
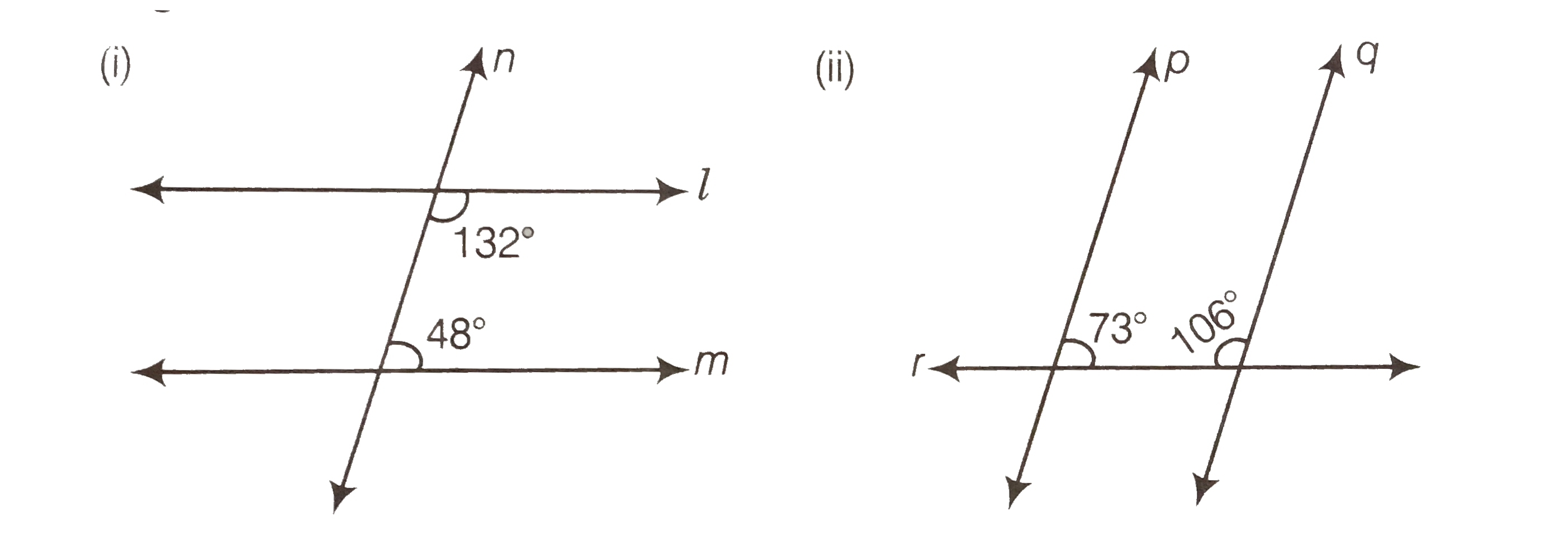
View SolutionIf the bisectors of a pair of alternate angles formed by a transversal with two given lines are parallel, prove that the given lines are parallel.
View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines are parallel;prove that the given lines are parallel.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf the bisectors of a pair of corresponding angles formed by a transversal with two given lines lines are parallel, prove that the given lines are parallel.
View SolutionWrite the converse of, "if the corresponding angles formed by a transversal of two lines are congruent, then two lines are parallel."
View SolutionIf a transversal intersects two lines in such a way that a pair of consecuitive interior angles are supplementary; then two lines are parallel.
View SolutionIf a Transversal intersects two lines in such a way that a pair of alternate interior angles are equal;then the two lines are parallel.
View SolutionCondition for Perpendicularity of two lines .
View Solution
