p(q2+r2)−q(r2+p2) can be factorised as
(P+q)(r2−pq)
(p−q)(r2−pq)
(p−q)(pq−r2)
(p−qr)(p+q)
The correct Answer is:B
To factorise the expression p(q2+r2)−q(r2+p2), we will follow these steps:
Step 1: Expand the expression
We start by expanding the expression:
p(q2+r2)−q(r2+p2)=pq2+pr2−qr2−qp2
Step 2: Rearrange the terms
Next, we rearrange the terms to group similar ones:
pq2−qp2+pr2−qr2
Step 3: Factor by grouping
Now we can factor by grouping. We will group the first two terms and the last two terms:
(pq2−qp2)+(pr2−qr2)
Step 4: Factor out common factors
From the first group pq2−qp2, we can factor out pq:
pq(q−p)
From the second group pr2−qr2, we can factor out r2:
r2(p−q)
So, we rewrite the expression as:
pq(q−p)+r2(p−q)
Step 5: Factor out the common binomial
Notice that both terms contain the factor (p−q):
(p−q)(pq+r2)
Final Result
Thus, the expression p(q2+r2)−q(r2+p2) can be factorised as:
(p−q)(pq+r2)
---
We start by expanding the expression:
p(q2+r2)−q(r2+p2)=pq2+pr2−qr2−qp2
Next, we rearrange the terms to group similar ones:
pq2−qp2+pr2−qr2
Now we can factor by grouping. We will group the first two terms and the last two terms:
(pq2−qp2)+(pr2−qr2)
From the first group pq2−qp2, we can factor out pq:
pq(q−p)
From the second group pr2−qr2, we can factor out r2:
r2(p−q)
pq(q−p)+r2(p−q)
Notice that both terms contain the factor (p−q):
(p−q)(pq+r2)
Thus, the expression p(q2+r2)−q(r2+p2) can be factorised as:
(p−q)(pq+r2)
Topper's Solved these Questions
- FACTORISATIONBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FACTORISATIONEXERCISE - QUESTION BANK -8
35 Videos
- DISTANCE TIME AND SPEED BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - DISTANCE TIME AND SPEED EXERCISE - SELF ASSESSMENT SHEET -14
10 Videos
- FRACTIONSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FRACTIONSEXERCISE - SELF ASSESSMENT SHEET-2
10 Videos
Similar Questions
Knowledge Check
Find the value of p2+q2r2+s2 , if p:q=r:s
A14B19CpqrsD(p−qr−s)2Find the value if p2+q2r2+s2 if p:q::r:s
A14BpqrsC(p+qr+s)2Dboth b and cIf (p2+q2)/(r2+s2)=(pq)/(rs), then what is the value of (p-q)/(p+q) in terms of r and s ?
A(r+s)/(r−s)B(r−s)/(r+s)C(r+s)/(rs)D(rs)/(r−s)
If Δ=∣∣ ∣ ∣∣0qrqrprpq∣∣ ∣ ∣∣, then ∣∣ ∣ ∣∣rq−p2pr−q2pq−r2rp−q2pq−r2rq−p2pq−r2rq−p2pr−q2∣∣ ∣ ∣∣ is equal to
View SolutionIf p = -2, q = - 1 and r = 3, find the value of
(i) p2+q2−r2
(ii) 2p2−q2+3r2
(iii) p - q - r
(iv) p3+q3+r3+3pqr
(v) 3p2q+5pq2+2pqr
(vi) p4+q4−r4
View SolutionIn the given quadrilateral ABCD , p∘+q∘=1002, a∘=140∘ and r∘=12(a2+q∘). Find the angles p∘,q∘,r∘ and s∘.
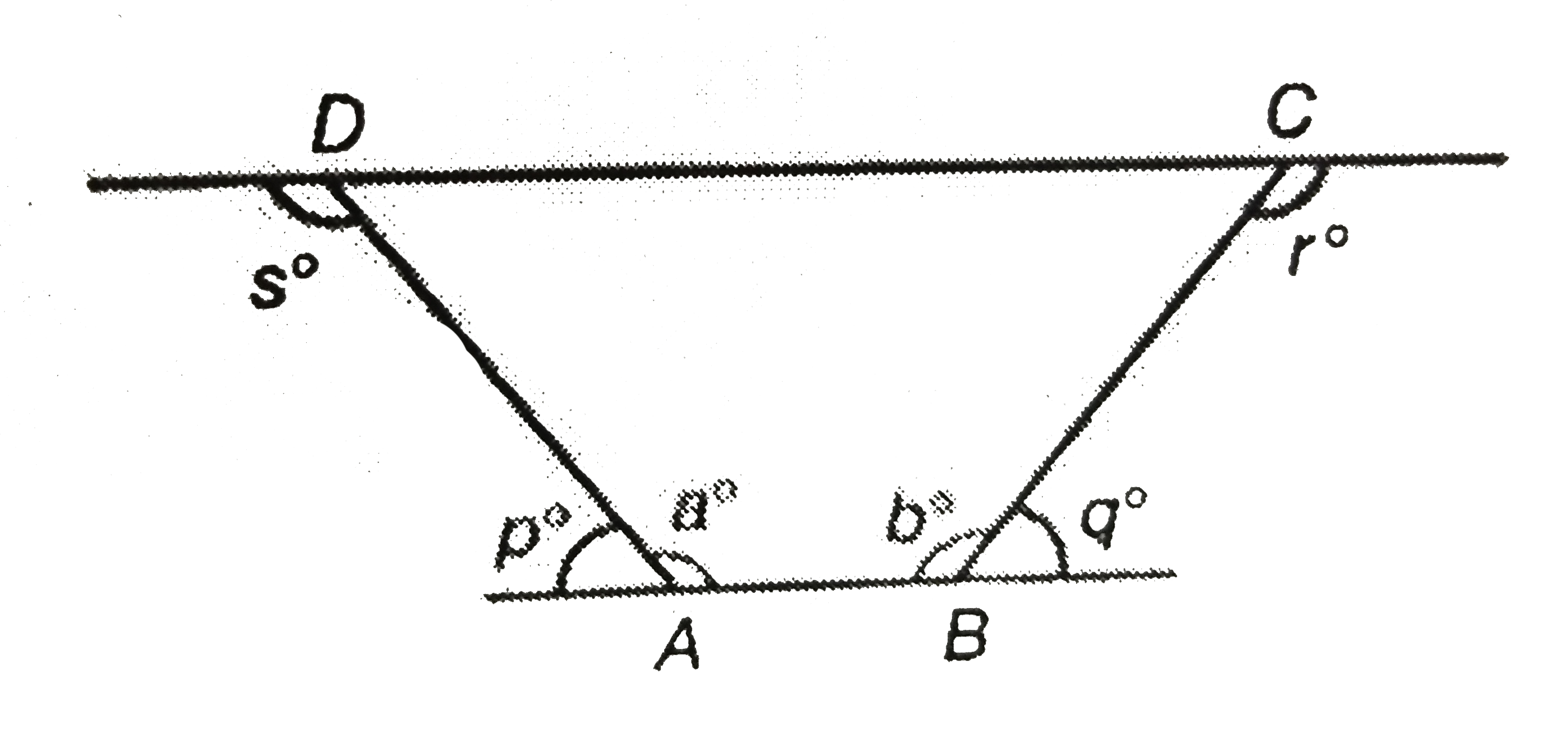
View SolutionIf pa+qb=rc=1andap+bq+cr=0 where p,q,r and a,b,c are non-zero, then the value of p2a2+q2b2+r2c2 is:
View SolutionIf pa+qb+rc=1 & ap+bq+cr=0 find p2a2+q2b2+r2c2= ?
View Solution