The function f(x)=x38−s∈πx+4∈[−4,4] does not take the value −4 b. 10 c. 18 d. 12Solution in Bengali
−4
10
18
12
The correct Answer is:C
f(x)=x38−sinπx+4
f(−4)=−4,f(4)=12
⇒f(x) can take value 10 as f(x) is continuous function
x38+4<12and|sinπx|≤1∀x∈[−4,4]
∴f(x) cannot take the value 18
Topper's Solved these Questions
Similar Questions
Given that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionThe value of f(0) so that the function ((1+x)^((1)/(3))-(1+x)^((1)/(4)))/(x) becomes continuous at x=0 is (A) (1)/(12) (B) (7)/(12) (C) 0 (D) 12
View SolutionIf f(x)=x4tan(x3)−x1n(1+x2), then the value of d4(f(x))dx4 at x=0 is 0 (b) 6 (c) 12 (d) 24
View SolutionThe function f(x)=x38−sinπx+4 in [−4,4] does not take the value −4 b. 10 c. 18 d. 12
View SolutionLet S be the area enclosed by the curves f(x)=4|x|-|x|^(3) and g(x)+sqrt(4-x^(2))=0 The value is equal to (A)10(B)12(C)14(D) 16
View SolutionIn(-4,4) the function f(x)=int_(-10)^(x)(t^(4)-4)e^(-4t)dt has
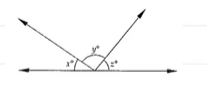
View SolutionIn Figure, if yx=5 and zx=4, then the value of x is (a) 80 (b) 180 (c) 120 (d) 150
View Solution(B)3(A)4. If the largest value of a for which fisi04Letf:10, al vec S be a function defined by f(x)= 3cosinverse function f-'(x) is kn, then the value of k is(D) 2(A);(B)1Cotion such thals
View SolutionValue of 4! -3! _______. (a) 24 (b) 6 (c) 12 (d) 18
View SolutionThe function f satisfies the functional equation 3f(x)+2f(x+59x−1)=10x+30 for all real x≠1. The value of f(7)is (a) 8 (b) 4 (c) −8 (d) 11
View SolutionThe function f satisfies the functional equation 3f(x)+2f(x+59x−1)=10x+30 for all real x≠1. The value of f(7)is 8 (b) 4 (c) −8 (d) 11
View SolutionThe function f(x)=x38−sinπx+4 in [−4,4] does not take the value −4 b. 10 c. 18 d. 12
View Solution(-4,4) Function in f(x)=int_(-10)^(x)(t^(4)-4)e^(-4t)dt Belongs to
View SolutionThe function f(x)=3x−2x+4 has an inverse that can be written in the form f−1(x)=x+bcx+d. The value of (b+c+d) equals
View SolutionLet S be the set of all x such that x4−10x2+9≤0 . The maximum value of f(x)=x3−3x on S, is 16 (b) 17 (c) 18 (d) 19
View Solution
