Let f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0Solution in Bengali
g(x) is an odd function
g(x) is an even function
graph of f(x) is symmetrical about the line x = 1
f'(1)=0
The correct Answer is:B, C, D
We have f(x)=f(2−x)
Replacing x by f(1+x), we get
f(1+x)=f(1−x)
Hence graph of f(x) is symmetrical about the line x = 1.
Also g(x)=f(1+x)=f(1−x)=g(−x)
∴ g(x) is an even function.
Further f'(1+x)=−f'(1−x)
∴ f'(1)=−f'(1)
∴ f'(1)=0
Topper's Solved these Questions
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- EQUATION OF PLANE AND ITS APPLICATIONS -IIBOOK - CENGAGE PUBLICATIONCHAPTER - EQUATION OF PLANE AND ITS APPLICATIONS -IIEXERCISE - DPP 3.4
8 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.18
1 Videos
Similar Questions
Let f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionLet A(0,6,6), B(6,6,0) and C(6,0,6) are three points and point D is moving on the line x+z−3=0=y. If G is centroid of ΔABC, then minimum value of GD is
View SolutionFollowing is the graph of y = f'(x) and f(0) = 0 .
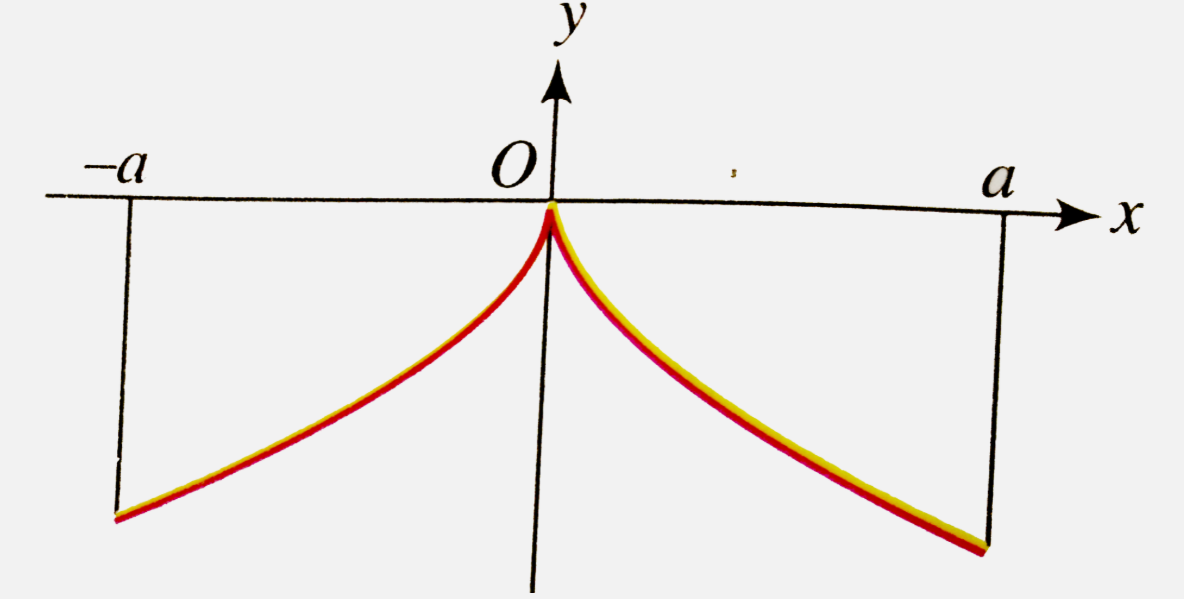
(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?
View SolutionLet f be a differential function such that f(x)=f(2-x) and g(x)=f(1+x) then (1) g(x) is an odd function (2)g(x) is an even function (3) graph of f(x) is symmetrical about the line x=1 (4) f'(1)=0
View SolutionLet f(x)=|x-2|+|x-3|+|x-4| and g(x)=f(x+1). Then 1.g(x) is an even function 2.g(x) is an odd function 3.g(x) is neither even nor odd 4.g(x) is periodic
View SolutionLet g(x) be the inverse of the function f(x) and f'(x)=(1)/(1+x^(3)) then g'(x) equals
View SolutionLet f:(−5,5)→R be a differentiable function of with f(4)=1,f'(4)=1,f(0)=−1andf'(0)=Ifg(x)=(f(2f2(x)+2))2, then g'(0) equals
View SolutionLet f:(−5,5)→R be a differentiable function of with f(4)=1,f'(4)=1,f(0)=−1andf'(0)=Ifg(x)=(f(2f2(x)+2))2, then g'(0) equals
View SolutionLet f(x)andg(x) be two differentiable functions, defined as:
f(x)=x2+xg'(1)+g''(2)andg(x)=f(1)x2+xf'(x)+f''(x).
The value of f(1)+g(−1) is:
View SolutionLet g(x) be the inverse of the function f(x) ,and f'(x)11+x3 then g(x) equals
View SolutionIf f(x)=x3andg(x)=x2+1, which of the following is an odd functionn (are odd functions)?
I. f(x)⋅g(x)
II. f(g(x))
III. g(f(x))
View SolutionLet f(x) be a function satisfying f'(x)=f(x) with f(0)=1 and g(x) be the function satisfying f(x)+g(x)=x2.Prove that,
∫10f(x)g(x)dx=12(2e−e2−3)
View SolutionLet f(x), g(x) be differentiable functions and f(1) = g(1) = 2, then : limx→1f(1)g(x)−f(x)g(1)−f(1)+g(1)g(x)−f(x) equals :
View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
View SolutionLet f:(−5,5)→R be a differentiable function of with f(4)=1,f'(4)=1,f(0)=−1andf'(0)=Ifg(x)=(f(2f2(x)+2))2, then g'(0) equals
View Solution
