For what real values of $a$ do the roots of the equation $x^{2} - 2 x - (a^{2} - 1) = 0$ lie between the roots of the equation $x^{2} - 2 (a + 1) x + a (a - 1) = 0 .$ Solution in Bengali

Video Solution

Text Solution

Verified by Experts

$f_{1} (x) = x^{2} - 2 x - (a^{2} - 1) = 0$ (1)
$f_{2} (x) = x^{2} - 2 (a + 1) x + a (a - 1) = 0$ (2)
From (1), we have
$x = \frac{2 \pm \sqrt{4 + 4 (a^{2} - 1)}}{2} = 1 \pm a$
Now, roots of (1) lie between roots of (2). Hence, graphs of functions $f_{1} (x) and f_{2} (x)$ are as follwos :

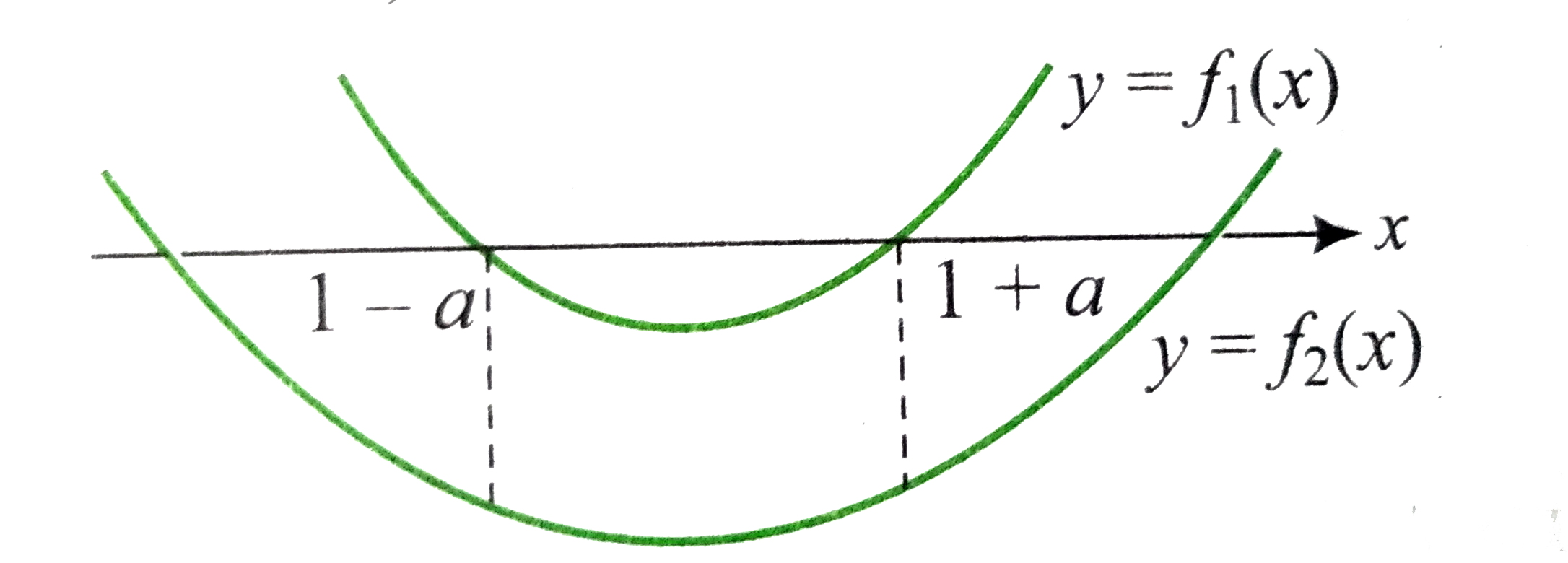
From the graph, we have
$f_{2} {(1 - a)}^{2} - 2 (a + 1) (1 - a) + a (a - 1) < 0$
$\Rightarrow {(1 - a)}^{2} - 2 (a + 1) (1 - a) + a (a - 1) < 0$
or $(1 - a) [(1 - a) - 2 a - 2 - a] < 0$
or $(1 - a) (- 4 a - 1) < 0$
or $(a - 1) (4 a + 1) < 0$
or -(1)/(4) lt a lt 1 $(3) < b r > and$ (1 + a)^(2) -2 (a +1)(a+1)+a(a-1) lt0 $< b r > or$ -(a+ 2)^(2) + a (a - 1) lt 0 $< b r > or$ -a^(2) - 2a - 1 + a^(2) -a lt 0 $< b r > or$ 3a + 1 gt 0 $< b r > or a$ gt - (1)/(3) $(4) < b r > F r o m (3) and (4), t h e r e q u i r e d v a l u e s o f a a r e$ ((-1)/(4), 1)

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-THEORY OF EQUATIONS-ILLUSTRATION

Home
Ask Doubt
Profile